8va Competencia
de Clubes Cabri
Segunda Ronda
15 de agosto de 1998
| nivel A |
1
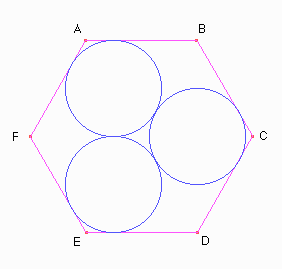
Construir la siguiente figura donde ABCDEF es un hexágono regular y las tres circunferencias tiene el mismo radio.

2
Dividir un triángulo equilátero en partes de forma tal que con dichas partes se forme un hexágono cuasirregular.
Nota: Un hexágono cuasirregular cumple que todos sus ángulos miden lo mismo y existen dos lados cortos, iguales entre si, que miden la mitad que los otros cuatro lados largos, iguales entre si.
3
A partir de un cuadrado ABCD, construir un cuadrado EFGH interior que cumpla que AB // EF, BC // FG, CD // GH y DA // HE. (Ojo al mover ABCD, EFGH debe seguir cumpliendo dichas condiciones.)
4
Prolonguemos los lados de EFGH formando 8 rectángulos, numerémoslos de la siguiente manera: 1 el de diagonal AE, 2 el de lado EF, 3 el de diagonal FB,…,8 el de lado EH. Probar que la suma de los perímetros de 1 y 5 es lo mismo que la de 3 y 7.Probar que la suma de las áreas de 2 y 6 es lo mismo que la de 4 y 8.
| nivel B |
5
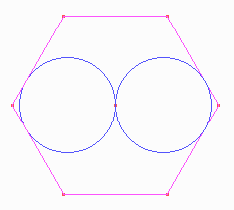
Construir la siguiente figura donde el hexágono es regular y las dos circunferencias tangentes al mismo tienen igual radio.
6
Dado un triángulo ABC equilátero, sea P un punto en su interior. Se traza la recta por P paralela a BC que corta a AB en D y a AC en E. Se traza la recta por P paralela a CA que corta a BC en F y a AB en G. Se traza la recta por P paralela a AB que corta a BC en H y a CA en I. Hallar la relación entre la suma de los perímetros de AGPI, BHPD, CEPF y el perímetro de ABC.
7
Dado un rectángulo ABCD (AB>BC), construir con regla y con compás puntos P en AB y Q en BC de manera que los triángulos DPQ y DCQ sean congruentes.
8
Construir un rectángulo ABCD que cumpla que CQ es el doble de BQ, definidos Q y P como el problema anterior.
| nivel C |
9
Dado un triángulo isósceles ABC (AB=BC), con un punto P en AC. Se trazan las paralelas por P a AB y BC obteniéndose como intersección los puntos D y E con los lados AB y BC respectivamente. Sea Q la intersección (distinta de P) entre las circunferencias de centros D y E que pasan por P. Hallar el LG de Q si P se mueve en AC.
10
Dado un cuadrado ABCD de centro O, y un punto P en AB. Sea Q en CD tal que P, O Q estén alineados y sea R en BC tal que PR perpendicular a RQ. Probar que PR + RQ es constante.
11
Dado un rectángulo ABCD y un punto P en su interior. Se traza las paralelas por P a AB y BC cortando en E, F, G y H a los lados AB, BC, CD y DA. Probar que las bisectrices de los ángulos AEP, BFP, CGP, DHP forman un rectángulo. Hallar el área del mismo si el área de ABCD es 1998.
12
Dado un cuadrado ABCD de centro O, sea P un punto en su interior. Se traza el cuadrilátero EFGH de los circuncentros de los triángulos PAB, PBC, PCD y PDA. De la misma forma se traza el cuadrilátero IJKL de los circuncentros de los triángulos OEF, OFG,OGH y OHE. ¿Que tipo de cuadrilátero es IJKL?
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |