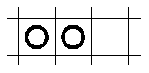
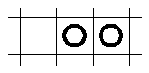
Podés bajar el cuento para verlo con WinWord (ranaword.zip) o el zip de este html con las imágenes (ranahtml.zip). Este cuento que te presentamos acá está sacado del libro Cuentos con Cuentas, de Miguel de Guzmán, que acaba de ser publicado por Red Olímpica. "El juego y la belleza están en el origen de una gran parte de la matemática. Si los matemáticos de todos los tiempos se lo han pasado tan bien jugando y contemplando su juego y su ciencia, ¿por qué no tratar de aprenderla y comunicarla a través del juego y la belleza?" Miguel de Guzmán La rana saltarina Tal vez conozcas el juego de la rana saltarina. Si no es así, tanto mejor. Para jugarlo puedes hacerte en un papel bien grande una cuadrícula de cuadros grandes en los que quepa una peseta. En la cuadrícula señalarás una línea horizontal gruesa a cinco cuadros de la línea horizontal superior. Algo así:
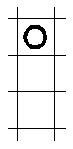
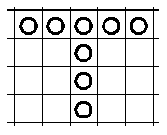
El juego consiste en lo siguiente. Colocas al principio un número de pesetas, el que quieras, distribuidas como te parezca mejor, cada una en algún cuadro de los de debajo de la raya gorda. Una vez colocadas vas a empezar a mover y retirar pesetas del tablero. Se puede mover sólo horizontalmente (a derecha e izquierda) y verticalmente (hacia arriba) saltando por encima de otra contigua siempre que el cuadro al que se salta esté vacío, comiendo (retirando) la moneda sobre la que se ha saltado. Por ejemplo, de esta situación
se puede pasar a esta otra
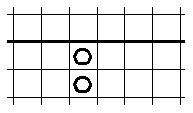
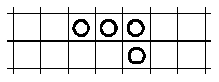
o de ésta
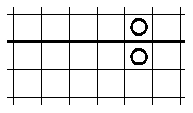
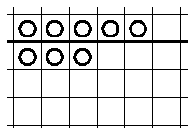
a esta otra
Se trata de colocar al principio las fichas o monedas debajo de la raya de modo que logres colocar una moneda con los movimientos permitidos lo más alta posible por encima de la raya gorda. Cuando hayas practicado un poco puedes tratar de hacerlo con el mínimo número de monedas. Por ejemplo, para llegar a la fila primera por encima de la raya gruesa es claro que con una sola moneda no lo consigues (no te permite ningún movimiento) pero con dos colocadas así
sí que lo puedes hacer. El mínimo número suficiente de monedas para colocar una en la primera fila de arriba es 2. Ponte a trabajar. ¿Cómo llegar a la fila 2? ¿Cuál será el número mínimo? ¿Y a la fila 3, 4, etc.? No quiero quitarte el gusto de hallarlo por ti mismo. Cierra y sólo después de un rato de jugar vuelve conmigo. Pronto habrás descubierto que para poner una peseta en la fila 2 tienes que llegar a esta situación.
Para llegar a ella te es suficiente colocar cuatro fichas en esta situación
Es fácil ver que con tres no puedes llegar a la segunda fila. Para llegar a la fila 2 el número mínimo suficiente es 4. ¿Y para la fila 3? La idea sería colocar inicialmente las fichas de modo que podamos llegar a la posición
o a su simétrica, pues así ya sabemos que podemos subir dos filas más. ¿Cómo podemos hacerlo? Como las cosas se van complicando más, lo mejor es tratar de inventar un modo sistemático de proceder. Éste puede ser uno bien razonable: jugar hacia atrás. Es decir, nuestra rana se va a mover al segundo cuadro hacia abajo o al segundo cuadro hacia la derecha o izquierda poniendo una peseta en el cuadro inmediato de la misma dirección, suponiendo siempre que éste esté libre. Es decir, de esta situación
se puede pasar a ésta
y de ésta
a ésta
Mediante estos movimientos hemos de tratar de colocar las piezas que resultan de esta situación.
todas ellas por debajo de la línea gruesa. Si pruebas un poco con este sistema verás que llegas enseguida a esta situación
desde la que, jugando al derecho, pasas a la fila tercera. Son ocho monedas. ¿Puedes demostrar que no se puede hacer con menos? Es curioso observar que a la tercera fila se puede llegar también de la situación siguiente, también de ocho monedas
sin necesidad de pasar por la situación intermedia correspondiente al salto hacia la segunda fila hacia arriba
y así, esta posición inicial en forma de T no resulta por el procedimiento de jugar al revés. Resumamos nuestros hallazgos:
Parece que se puede decir: Malo será que para la fila 4 no sea 24 el número mínimo, ¿no? Pues, por malo que parezca, así sucede. Para llegar a la fila 4 será suficiente (no necesario, en principio, como hemos visto que sucedía con la fila 3) partir de una situación inicial de la cual podamos llegar a una de las posiciones
o, naturalmente, a la simétrica de la primera. Jugando al revés y con cierto cuidado para no introducir fichas superfluas, verás que la situación A y la situación B te pueden llevar a la situación inicial siguiente
Pero la situación A te puede llevar también, jugando al revés, a ésta,
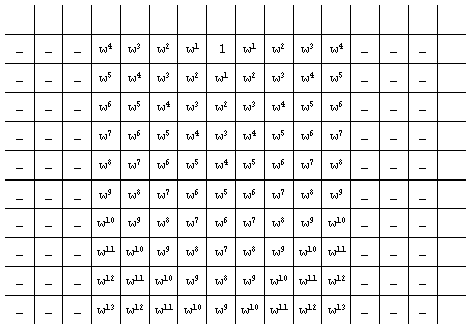
que es distinta de la anterior, pero ambas tienen 20 monedas. ¿Se podrá llegar con menos? ¿Por qué no lo intentas? ¿Y para la fila 5? Adelante. Verás que con menos de 20 monedas no logras llegar a la fila 4. Para la fila 4 el número mínimo es 20, lo que enseña que no hay que fiarse demasiado de inducciones prematuras. ¿Y para la fila 5? Ya no pisamos terreno firme para hacer una conjetura. Pues bien, aunque parezca sorprendente, a la fila 5 no se puede llegar con ningún número de fichas, colóquense donde se quieran colocar. La demostración siguiente se debe a John Conway, de Cambridge. Tomamos el número positivo w tal que w2 + w = 1. Misterioso, ¿no? Pues resulta que, para mayor desconcierto, w es el inverso del número áureo j > 0 tal que j / 1 = (j + 1) / j Ponemos en cada casilla de nuestro tablero indefinidamente prolongado hacia abajo y a la derecha e izquierda una potencia de w tal como te indico en la figura siguiente.
Observa ahora los dos hechos siguientes: a) La suma de todos los números que figuran bajo el eje es S = (w5 + w6 + w7 + ...) + 2 (w6 + w7 + ...) + + 2 (w7 + w8 + w9 + ...) + ... = = w5 / (1 - w) + 2 (w6 / (1 - w)) + 2 (w7 / (1 - w)) + ... y como 1 - w = w2, resulta S = w3 + 2 w4 + 2 w5 + ... = = (w3 + w4 + w5 + ...) + (w4 + w5 + w6 + ...) = = w3 / (1 - w) + w4 / (1-w) = w + w2 = 1 S = 1 Así, la suma de los números correspondientes a un número finito de casillas es estrictamente menor que 1. b) Interpretemos ahora nuestros movimientos permitidos con las pesetas en relación con estos números del modo siguiente. Sumamos los números correspondientes a casillas del tablero ocupadas por pesetas antes y después de un movimiento. Por ejemplo,
Otro caso
w9 + w8 = w7 > w10 Este hecho, como fácilmente percibirás, es general, es decir, la suma correspondiente a casillas ocupadas es la misma o menor a lo largo de todos nuestros posibles movimientos. Ahora bien, la suma correspondiente a casillas ocupadas al comenzar el juego (un número finito de casillas ocupadas) es, como hemos visto, menor que 1. Si con nuestros movimientos lográsemos llegar a la quinta fila, colocando nuestro 1 en ese cuadro de la quinta fila que se alcanza, resulta que la suma correspondiente a casillas ocupadas al final sería mayor o igual que 1, lo cual es imposible. La idea de Conway es muy ingeniosa. ¿Por qué no tratas de explotarla para aclarar algunas de las preguntas que han quedado colgando? Un poco de álgebra te ayudará. 1) Demuestra que, efectivamente, el número mínimo de fichas para llegar a la fila 3 es 8 y para la fila 4 es 20. Esto último no es fácil. 2) Demuestra si las únicas posiciones iniciales para llegar a la fila 3 y 4 son las señaladas y sus simétricas. 3) Plantéate otros problemas semejantes como por ejemplo si se puede, y cómo, llegar a las situaciones
Y te pediría que me escribas si tienes alguna idea sugerente sobre todo este lío. Gracias. (Si querés escribirle, podés hacerlo. Su dirección electrónica es mdeguzman@bitmailer.net) Notas El número áureo, que aparece en este capítulo, ha sido desde la Antigüedad un número misterioso que aparece en situaciones extrañamente diversas. La sección áurea de los monumentos clásicos, neoclásicos y modernos es la proporción geométrica en la que un punto interior P de un segmento AB divide al segmento de tal forma que AB / AP = AP / PB. Resulta así para AB / AP el valor 1,618... que se denomina número áureo. Una de las situaciones curiosas en que aparece el número áureo es la siguiente. Leonardo de Pisa, el matemático más importante de la Edad Media (nació hacia 1170), también llamado Fibonacci, propuso en su obra más importante, Liber Abaci, donde introdujo los numerales arábigos en Occidente, el siguiente problema curioso: "Cierto hombre puso un par de conejos en un lugar rodeado por todas partes por una valla. ¿Cuántos pares de conejos se engendran a partir de aquel par en un año, suponiendo que cada par engendra cada mes un nuevo par que resulta productivo a partir del segundo mes?". La sucesión del número de pares que hay en cada uno de los sucesivos meses, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ..., en la que cada término es la suma de los dos anteriores, se denomina la sucesión de Fibonacci. Pues bien, la razón de cada término de la serie de Fibonacci al siguiente se aproxima cada vez más al número áureo (el límite de esta razón es precisamente el número áureo). |