10ma
Competencia de Clubes Cabri
Segunda Ronda
5 de junio de 1999
Duración: 2.30hs
| nivel A |
1
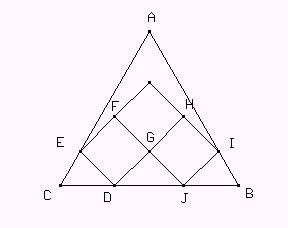
Construir la siguiente figura, donde ABC es un triángulo equilátero y DEFG y GHIJ son cuadrados y el ángulo FGH es recto.

2
Sea ABC un triángulo rectángulo isósceles, con Ð A = 90°. Construir un punto P en AB tal que la circunferencia de centro P, que pasa por A sea tangente a BC.
3
Sea ABC un triángulo, sea M el punto medio de AB y sea P el punto medio de CM. Sabiendo que CM = AB y que PA = 1 y PB = 2. Hallar la longitud de la altura desde C del triángulo ABC.
4
Sea ABC un triángulo cualquiera y sea M el punto medio de AB. Construir un triángulo isósceles DEF (DE = EF) que tenga igual área que ABC y de modo que la mediana de DEF correspondiente al lado DF sea igual a CM.
NOTA: la mediana de DEF correspondiente al lado DF es el segmento que une el punto medio de DF con el vértice E.
| nivel B |
5
Sea ABC un triángulo y sean r y t las bisectrices de los ángulos Ð A y Ð B respectivamente. La recta que pasa por los puntos medios de AC y BC interseca a r y t en M y N respectivamente. Demostrar que la circunferencia circunscripta al triángulo CMN pasa por el incentro de ABC.
6
Sea ABC un triángulo y P un punto sobre AB. Sea M el punto medio de CP y sea N el punto medio de MA. Hallar el lugar geométrico de N a medida que P se mueve sobre el segmento AB.
7
Dado un triángulo PQR construir una circunferencia C que cumpla con las siguientes condiciones:
8
Construir un triángulo ABC que cumpla con las siguientes condiciones:
| nivel C |
9
Dado el cuadrilátero convexo ABCD, sean M y N los puntos medios de AC y BD respectivamente. Sean O, P, Q y R los puntos medios de NA, MB, NC y MD respectivamente.
10
Sea K una circunferencia y sean A, B y C puntos sobre ella. Sea r la bisectriz de <BAC, s la perpendicular a r que pasa por B y t la perpendicular a r que pasa por C. Sea P la intersección entre r y s. Sea Q la intersección entre r y t. Sea O el punto medio de PQ. Hallar el lugar geométrico de O a medida que A se mueve por K.
11
Sea ABC un triángulo acutángulo y sean D y E los pies de las alturas desde A y B respectivamente. Sabiendo que DE = 3 y AB = 5 hallar la suma de las áreas de los triángulos DEA y DEB.
12
Construir el triángulo ABC sabiendo que Ð A = 60° y que el perímetro del triángulo es igual a 4 veces la altura desde A.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |