11ma
Competencia de Clubes Cabri
Segunda Ronda
2 de octubre de 1999
Duración: 2.30hs
| nivel A |
1
Sea ABCD un rectángulo. M y N son los puntos medios de AD y BC respectivamente. Sean P y Q en AB y MN respectivamente de modo que PQ // AD. Si el perímetro de APQM es 7 y el perímetro de ABCD 15, ¿cuál es el perímetro de PBQN?
2
Sea ABC con AB = AC. La bisectriz de ABC interseca a AC en D. La bisectriz de BDC interseca a BC en E. Sabiendo que DE = CD hallar los ángulos interiores de ABC.
3
Sea ABCD un rectángulo tal que AB = 2 y BC = 1. Sea M el punto medio de CD. Hallar la distancia de M a la recta AC.
4
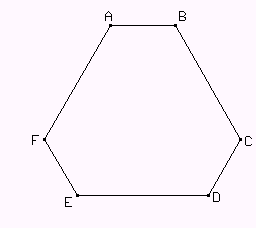
Construir un hexágono ABCDEF con todos sus ángulos de 120° tal que AB = CD = EF = 1 y BC = DE = FA = 2.

5
Dividir el hexágono del problema 4, en 4 piezas de modo que con ellas se puedan armar (sin agujeros ni superposiciones) dos triángulos equiláteros (no necesariamente iguales). Hallar los lados de los dos triángulos equiláteros formados.
| nivel B |
6
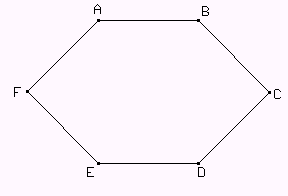
a) Construir un hexágono ABCDEF de modo que todos sus lados midan 1 y tal que BCD = EFA = 90° y los ángulos ABC = CDE = DEF = FAB.
b) Hallar la medida de AD.
7
Sea ABC un triángulo de área 1. Sea D el simétrico de C con respecto a A, sea E el simétrico de D con respecto a B y sea F el simétrico de E con respecto a C.
a) Hallar el área de EFD.
b) Demostrar que ABC y CFD son semejantes.
8
Sea ABCD un cuadrilátero tal que ABC = 120°, BCD = 90° y CDA = 60° y además AB = 1 y CD = 2. Hallar las medidas de AD y de BC y construir la figura.
9
Sea ABCD un rectángulo. Sean APB y ADQ triángulos equiláteros exteriores al rectángulo. Demostrar que PQC es equilátero.
| nivel C |
10
Sea ABC un triángulo tal que si M es el punto medio de AB entonces 2CM = AC y de modo que MCB = 2ABC. Hallar los ángulos de ABC.
11
Se tiene una circunferencia C y un punto P en su exterior. Sea T en C tal que PT es tangente a la circunferencia. Sea Q un punto en C. La recta PQ interseca a C en Q y R. La bisectriz del ángulo QTR interseca a RQ en A. Hallar el lugar geométrico de A al moverse Q sobre C.
12
Son dadas dos rectas no perpendiculares, que se cortan en un punto y un segmento.
Construir un triángulo rectángulo tal que la suma de los catetos del triángulo sea igual al segmento dado y uno de los ángulos del triángulo sea igual al ángulo agudo que forman las dos rectas.
13
Dado un triángulo ABC acutángulo cualquiera, construir un rectángulo PQRS tal que P y Q estén en el lado AB, R esté en el lado BC, S esté en el lado AC, tal que la longitud de la diagonal sea mínima.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |