13ra
Competencia de Clubes Cabri
Segunda Ronda
14 de octubre de 2000
Duración: 2.30hs
| nivel A |
1
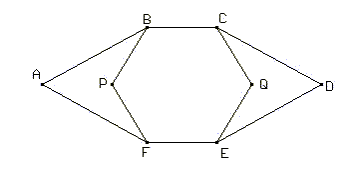
Construir la siguiente figura sabiendo que BCQEFP es un hexágono regular y que ABF y CDE son triángulos equiláteros.

2
Sabiendo que BC = 1 hallar las medidas de AB, AC y AD.
3
Cortar la figura ABCDEF en tres paralelogramos y demostrar que las piezas que quedaron son efectivamente paralelogramos. Hallar las áreas de dichos paralelogramos.
4
Sea M el punto medio de AF y N el punto medio de DE. La rectas MB y NC se cortan en el punto T. Hallar la medida del ángulo TDF.
5
Sea ABC un triángulo equilátero de lado 10. Sea P un punto sobre la prolongación de AB tal que AB = BP y sea Q un punto sobre la prolongación de AC tal que CQ = 2 AC (como se ve en la figura).
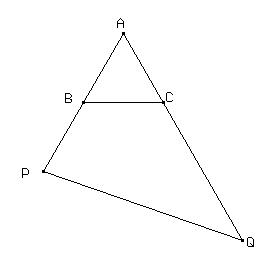
Hallar el perímetro del triángulo APQ.
| nivel B |
6
Dado un triángulo ABC, construir un triángulo DEF cuyos lados midan igual que las medianas de ABC. Calcular la relación entre las áreas de ABC y DEF.
7
Sea ABCD un cuadrado y P y Q dos puntos en su exterior tales que APB = 90° y BQC = 90°. Hallar el punto donde se cortan las bisectrices de APB y BQC.
8
Sea ABC tal que A = B = 30°. Sea P en AC y Q en AB de modo que PQ es perpendicular a AB. Hallar (PQ + PC) / QB.
9
Dado un triángulo equilátero ABC hallar el lugar geométrico de todos los puntos P del plano tal que las áreas de ABP y BCP sean iguales.
| nivel C |
10
Construir un triángulo acutángulo ABC tal que si H es la intersección de sus alturas entonces: área(ABH) = 1, área(ACH) = 2 y área(BCH) = 3.
11
Sea ABC un triángulo con AC = 2 BC. Sean M y N los puntos medios de AB y BC respectivamente. Hallar todos los triángulos ABC para los cuales la mediatriz de MB y la de NC se cortan sobre AC.
12
Sea ABCD un cuadrado. Sea E un punto en el segmento AD y sea F un punto en la recta CD de modo que EB sea perpendicular a BF. Si AB mide 2 y el área de EBF es el doble del área de DEF, hallar EB.
13
Sea ABCD un rectángulo y sean P y Q puntos en su exterior tal que APB = BQC = 90° tales que P, B y Q están alineados. Las bisectrices de APB y BQC se cortan en O. Hallar el lugar geométrico de O.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |