18va Competencia de Clubes Cabri
Segunda Ronda
Nivel Menor
Problema
N°1:
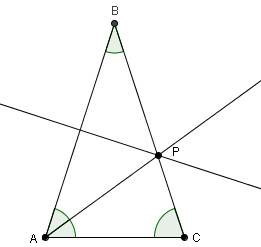
Sea ABC un
triángulo isósceles con AB = BC. La
bisectriz del ángulo BAC corta al segmento BC en P tal que BP = PA. Hallar los ángulos del triángulo ABC.
Solución de
“Taller el Triángulo”:
·
Como AP = PB,
entonces <BAP = <ABP = a.
·
Como AP es la
bisectriz del ángulo <BAC, entonces
<CAP = <BAP = a.
·
Como ABC es
isósceles, entonces <BCA = <BAC = <BAP + <CAP = 2·a.
Ya colocados
todos los valores de los ángulos del triángulo ABC en función de una misma
incógnita, y sabiendo que la suma de los ángulos interiores de un triángulo es
igual a 180º, podemos plantear:
180º = <ABC
+ <BAC + <BCA = a + 2·a + 2·a =
5·a
De donde a = 36º,
ahora se pueden averiguar los ángulos del triángulo ABC efectuando las
siguientes operaciones:
Ángulo BAC =
36º.2 = 72º
Ángulo ACB = 36º.
2 = 72º
Ángulo ABC = 36º
Problema N°2:
a) Indicar los pasos para construir la siguiente
figura de forma que todos los segmentos dibujados sean iguales.
(Es
decir, de forma que AB=BC=CD=DE=EA=GB=GA=GE=FB=FC=FD).
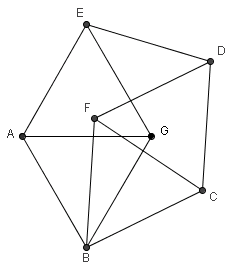
b) Demostrar que
si a cada punto del plano lo pintamos de un color, y sólo disponemos de tres
colores para elegir, entonces, sin importar la forma en que lo hagamos, siempre
habrá dos puntos del mismo color que estén a distancia 1.
Solución de “Los discípulos de Maite”:
a) Primero veamos cómo construir la figura y después
veamos que se verifican las condiciones:
1. Se marca un segmento FC.
2. Se trazan las circunferencias con centros en F y C y
radios FC que se cortan en B y D.
3. Se trazan las circunferencias con centros en D y B y
radios CD y BD respectivamente que se cortan en E y H. 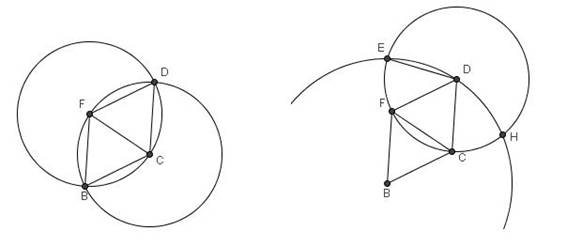
4. Se trazan las circunferencias con centros E y B y
radios ED y BC respectivamente que se cortan en A y G.
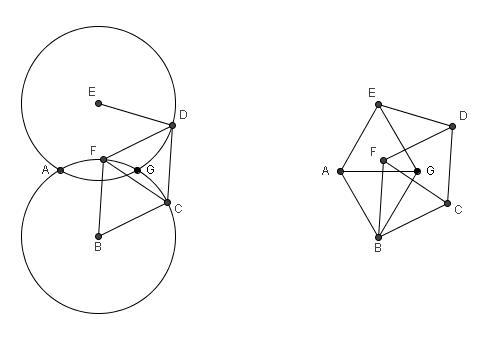
Para ver que se verifican
las condiciones notemos que
1.
Como B y D están
en las circunferencias de centros F y C y radios FC entonces FB = FD = BC = DC
= FC.
2.
Como E está en
la circunferencia de centro D y radio CD luego ED = CD.
3.
Como A y G están
en las circunferencias de centros E y B y radios ED y BC entonces AE = AB = GE
= GB = FC (notar que ED = CD = BC).
4.
Como E está en
la circunferencia de centro B y radio BD entonces BE = BD de donde los rombos
BCDF y BGEA son iguales (pues tienen los cuatro lados y una diagonal iguales).
5.
Como los rombos
BCDF y BGEA son iguales entonces AG = FC.
En
conclusión FB = FD = BC = DC = FC = DE = AG = AE = AB = GE = GB como queríamos.
b) Vamos a
suponer que los colores son verde, azul y rojo.
Tomamos la figura de la primera parte con BA
= BG = BC = CD = DE = EA = GA = GE = FB = FC = FD = 1. Si se pudiese pintar a
cada punto del plano con uno de los 3 colores sin que haya dos puntos del mismo
color a distancia 1 entonces en particular no puede haber 2 puntos del mismo
color conectados en la figura de la primera parte.
Sin
perder generalidad podemos pensar que el punto B esta pintado de rojo y que el
punto A de azul (AB = 1 de donde no pueden estar ambos del mismo color). Como AG = 1 y BG = 1 (mirar figura del medio)
entonces G no puede ser ni azul ni rojo entonces debe ser verde. Como AE = GE =
1 entonces E no puede ser ni azul ni verde entonces debe ser rojo. Como BF = 1
luego F puede ser azul o verde.
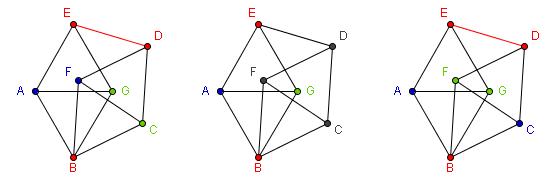
Si F es azul (figura de la izquierda), como
FC = BC = 1, luego C tiene que ser verde pero FD = CD = 1 entonces D tiene que
ser rojo. Pero entonces E y D son ambos rojos con ED = 1 lo que es imposible.
Si F es verde (figura de la derecha), como FC
= BC = 1, luego C tiene que ser azul, pero FD = CD = 1 entonces D tiene que ser
rojo, lo que vuelve a resultar imposible ya que ED = 1 con E y D son rojos.
Hemos probado entonces que es imposible
pintar los puntos de la figura propuesta de rojo, azul o verde de modo que no
haya dos puntos del mismo color a distancia 1.
Nota: Es un problema famoso tratar de pintar a cada punto del plano usando la
menor cantidad posible de colores de modo que no haya dos puntos a distancia 1
del mismo color. Se sabe que 3 colores no alcanzan y se puede probar que con 7
colores es posible, sin embargo nadie sabe si 7 es la menor cantidad de colores
necesaria.
Problema N°3:
Sea ABCDE un pentágono convexo en el cual
ACE es un triángulo equilátero,
AB=BC=DE con <ABC=150º y <CED=45º. Si se sabe que AE=1, entonces:
a) Calcular BD
b) Probar que CD es paralelo a BE
c) Calcular el área de ABE
Solución de “Binomius”:
a)
Como AB = BC y <ABC = 150º entonces <BAC = <BCA = 15º. Ahora, en el cuadrilátero ABDE, como
<AED + <EAB = (60º + 45º) + (60º + 15º) = 180º entonces AB // DE, pero AB = DE, de donde
ABDE es un paralelogramo, con AB = DE y BD = AE = 1. Es decir que BD = AE = 1.
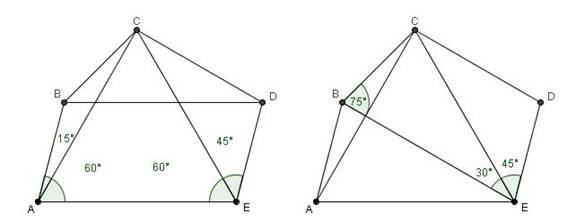
b)
Notemos que como ABCE es un romboide (AB = BC y AE = EC) entonces BE es la
bisectriz de <AEC de donde <BEC = 60º /2= 30º. Luego por lo anterior
<BED = 30º + 45º = 75º. Pero BE
también es bisectriz de <CBA entonces
<EBC = 150º /2 = 75º = <BED. Como BC = ED, luego el cuadrilátero
BCDE es un trapecio isósceles con CD // BE.
c) Como la recta BE es
mediatriz de AC, el problema se reduce a obtener la suma de la mitad del área
del triángulo AEC y la mitad del área del triángulo ABC, que en definitiva será
la mitad del área del romboide ABCE.
Como <CBE = 75º = <BCE entonces BEC
es isósceles con BE = CE = 1. Ahora,
Área (ABCE) = ½ · BE · AC = ½ · 1 · 1 = ½. Luego Área (ABCE) = ½ y Área (ABE) = ¼.