18va Competencia de
Clubes Cabri
Tercera Ronda
Nivel Menor
Duración: 4 horas
1) Sea ABC un triángulo equilátero y PQRS un cuadrado con P y Q en BC, R en CA y S en AB. Si se sabe que PQ = 3, calcular la medida del segmento AB y la del ángulo <PAS.
2) Sea ABC un triángulo, con M y N puntos medios de AB y AC, respectivamente. Sea además H el pie de la altura trazada por A en el lado BC.
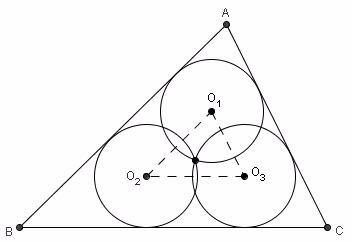
3) Sea ABC un triángulo y C1, C2 y C3 tres circunferencias de centros O1, O2 y O3, tales que C1 es tangente a AB y a AC, C2 es tangente a AB y a BC y C3 es tangente a AC y a BC. Se sabe además que las tres circunferencias tienen un punto en común, y que todas tienen el mismo radio, al que llamamos rc.

Una vez finalizada la prueba, las soluciones a los problemas deben enviarse por mail a la dirección clubescabri@oma.org.ar, colocando en el subject del mail el nombre de su club, el nivel al que corresponde y el código que les asignamos. Pueden enviar las respuestas en el mismo texto del mail, en archivo de Word o en archivo PDF. Pueden adjuntar todos los dibujos que hayan hecho con el programa de geometría que estén usando (.fig, .geo, etc) que les parezcan útiles para acompañar la explicación.
Deben estar justificados todos los razonamientos que los llevaron a la solución. Pueden enviar las ideas de problemas que no lograron terminar, ya que son consideradas a la hora de evaluar la prueba.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |