3era Competencia de Clubes Cabri
Segunda ronda
1er nivel
1. Dado un triángulo ABC construir el rombo BEFG sabiendo que E, F y G son puntos pertenecientes a cada uno de los lados del triángulo (uno por lado).
2. Dado un cuadrilátero ABCD (en ese orden) , hallar la medida de BDC si ABD = 45, DBC = 60 ; BAC = 30 , CAD = 60.
3. Dado un triángulo ABC equilátero , sea A+ el simétrico de A con respecto a B, sea A- el simétrico de A con respecto a C; sea B+ el simétrico de B con respecto a C, sea B- el simétrico de B con respecto a A y sea C+ el simétrico de C con respecto a A, sea C- el simétrico de C con respecto a B. Se trazan las rectas A+ A- , B+ B- y C+ C- formándose el triángulo A’B’C’ en las intersecciones de dichas rectas. Probar que dichos triángulos son semejantes. Averiguar la razón de semejanza.( AB / A’B’).
4. Construir un trapecio isósceles ABCD (AB // CD) sabiendo que sus diagonales son perpendiculares y que AB = BD.
5. Dado un triángulo ABC, y un punto interior P, se trazan r, s y t rectas paralelas por P a los lados BC, AB y CA respectivamente. Sea F la intersección entre r y AB, sea G la intersección entre r y AC, sea D la intersección entre t y BC y sea E la intersección entre s y BC.
Hallar el lugar geométrico de los puntos P si las áreas de los paralelogramos GPDC y FPEB son iguales.
6. En el problema anterior, hallar el lugar geométrico de los puntos P si los perímetros de los paralelogramos GPDC y FPEB son iguales.
2do nivel
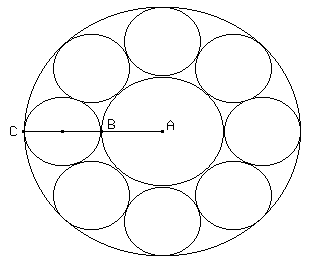
7. Construir la siguiente figura y calcular AB / BC.
8. Dado un cuadrilátero ABCD (en ese orden), hallar la medida de ACD si ABD = 30, DBC = 30; BAC = 60, CAD = 45.
9. Dadas dos circunferencias C1 y C2 de igual radio, un punto A en C1 encontrar puntos B y C en C2 de manera que ABC sea un triángulo equilátero.
10. ¿Qué condición y/o condiciones deben cumplirse para que exista el triángulo ABC del problema anterior?
11. Dado un triángulo, construir con regla y compás un cuadrado que tenga la misma superficie que el triángulo.
12. Dado un paralelogramo ABCD, sean E, F, G y H puntos sobre los lados DA, AB, BC y CD respectivamente y los puntos J e I en el interior del paralelogramo tales que AFJE Y CHIG son rombos y B, J, I y D están alineados. ¿Qué relación existen entre los lados del paralelogramo si se sabe que A, J, G y C, I, E también están alineados?
[ 3era Competencia - Ronda final ]
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |