6ta Competencia de Clubes Cabri
Ronda Final
1er nivel
1
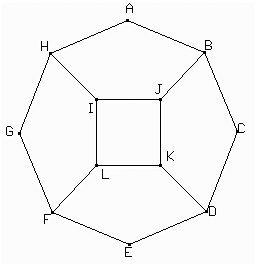
Construir la siguiente figura donde ABCDEFGH es un octógono regular y HI = BJ = DK = LF = lado del cuadrado IJKL.

Hallar y justificar la relación: ![]()
2
Sea ABCD un cuadrado y el punto P en su interior, se trazan las mediatrices de PA, PB, PC y PD formándose un cuadrilátero EFGH.
3
Dado un triángulo ABC, construir un punto D en BC de manera tal que si E pertenece a AC y DE es perpendicular a AC y F pertenece a AB y DF es perpendicular a AB entonces DEF es un triángulo isósceles.
4
Sea ABC un triángulo y CI el simétrico de C con respecto a A, CII el simétrico de CI con respecto a B, CIII el simétrico de CII con respecto a C, CIV el simétrico de CIII con respecto a A y CV el simétrico de CIV con respecto a B. Probar que CV coincide con C.
2do Nivel
5
Dado P, Q y R puntos del plano. Construir un triángulo equilátero ABC tal que P, Q y R pertenezcan a las semirrectas AB, BC y CA respectivamente, pero no pertenezcan al perímetro de ABC.
6
Dados dos segmentos AB y CD construir todos los triángulos ABS tales que si P en AS es tal que AP / AS = 1 / 4 y Q en BS es tal que BQ / BS = 3 / 4 entonces PQ = CD.
7
Sea ABC equilátero y P un punto sobre AB. Construir el cuadrado PQRS de modo que Q esté en CA y S esté en BC.
Hallar P para que el área de PQRS sea mínima.
8
Sea A1A2...A2n
un 2n-gono regular y un punto B1.
Sea B2 el simétrico de B1
con respecto A1.
Sea B3 el simétrico de B2
con respecto A2.
Sea B2n el simétrico de B2n-
1 con respecto A2n- 1.
i) Probar que A2n es punto medio de B1B2n.
ii) Demostrar que B1B3...B2n-1 y B2B4...B2n son n-gonos regulares iguales.
iii) Probar que el per(B1B3...B2n- 1) = per(B2B4...B2n) = per(A1A2...A2n).
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |