9na Competencia
de Clubes Cabri
Primera Ronda
18 al 28 de septiembre de 1998
| nivel A |
1
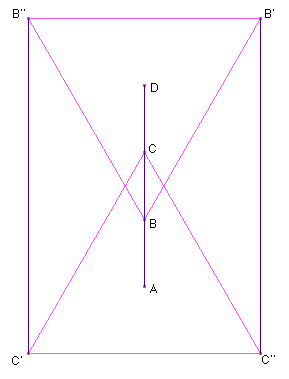
Construir la siguiente figura, donde AB = BC = CD. Además los triángulos BB’B’’ y CC’C’’ son equiláteros de centros D y A respectivamente.

2
Hallar la razón entre las medidas de los segmentos BC y B’C’’. Justificar.
3
¿Si el área de BB’B’’ es 27, cuál es el área de B’B’’C’C’’? Justificar.
4
Construir un cuadrilátero ABCD tal que CD = DA y sus ángulos ABC, BCD, CDA y DAB midan 30°, 90°, 120° y 120° respectivamente
5
En el problema anterior, probar que AB mide el triple que CD.
| nivel B |
6
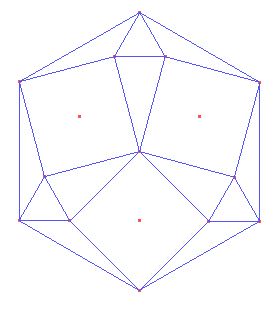
Construir la siguiente figura formada por un hexágono regular con tres cuadrados iguales y tres triangulos equilateros iguales en su interior.
7
Construir un rectángulo ABCD (en ese orden) tal que la circunferencia de centro A que pasa por B y la circunferencia de centro C que pasa por D sean tangentes entre sí.
8
Dado un triángulo genérico ABC, dividirlo en partes de forma tal que dichas partes se puedan reacomodar para formar dos rectángulos iguales, sin que sobren piezas.
9
Sea C una circunferencia de centro O y A un punto exterior a la circunferencia. Sea P un punto sobre C. Se traza la circunferencia D, de centro A que pasa por P y la recta r que pasa por O y P. La recta r corta a D en dos puntos (uno es P). Sea M el punto medio de estos dos puntos. Hallar el lugar geométrico de M al variar P sobre C.
10
Dado un cuadrilátero ABCD, construir con regla y con compás un rombo que tenga la misma superficie que ABCD (Explicar los pasos de la construcción.)
| nivel C |
11
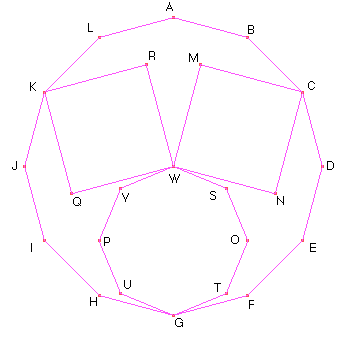
Construir la siguiente figura formada por un dodecágono regular con dos cuadrados y un octógono regular en su interior, siendo W el centro del dodecágono.
12
En las condiciones del problema anterior, probar que ARM, ENO y PIQ son triángulos equiláteros.
13
Dado un rectángulo ABCD de centro O, sea P un punto en CD. Se trazan las rectas perpendiculares por O a AP y BP cuyas intersecciones con las rectas BC y DA forman un cuadrilátero EFGH. ¿Qué tipo de cuadrilátero es EFGH? Justificar.
14
Construir un rectángulo ABCD tal que si P es el punto medio de CD, el cuadrilátero EFGH construido como en el punto anterior es un cuadrado.
15
A partir de un triángulo ABC, se construyen los puntos: D como intersección de las rectas perpendiculares a AB por B y AC por C; E como intersección de las rectas perpendiculares a BC por C y BA por A; F como intersección de las rectas perpendiculares a CA por A y CB por B. Probar que el triángulo DEF es semejante al ABC. ¿Cuál es su razón de semejanza?
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |