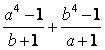 es
un número entero. Demostrar que
es
un número entero. Demostrar que 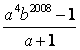 es
un número entero.
es
un número entero.19° Olimpíada
Matemática del Cono Sur
Prueba de Selección
27 y 28 de marzo de 2008
Primer día
1. Fede tiene 11 monedas aparentemente todas iguales. Sin embargo, Fede sabe que exactamente una de sus monedas es falsa, y que su peso es inferior al de las auténticas (todas las auténticas tienen pesos iguales). Para detectar la moneda falsa, Fede tiene una balanza de dos platos fallada: esta balanza se equilibra cuando el peso de los objetos colocados en el plato izquierdo es igual al doble del peso de los objetos colocados en el plato derecho. Demostrar que Fede siempre puede detectar la moneda falsa utilizando tres veces esta balanza.
2. Sean a y b enteros a
≠ - 1, b
≠ -
1, tales que 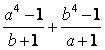 es
un número entero. Demostrar que
es
un número entero. Demostrar que 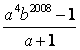 es
un número entero.
es
un número entero.
3. Alex y Fredy colorean por turnos las casillas de un tablero de n x n (n ≥ 2). Alex, en su turno, debe colorear de azul un cuadrado de 2 x 2 formado por 4 casillas del tablero tales que ninguna de ellas se haya coloreado anteriormente. Fredy, en su turno, colorea de rojo una casilla del tablero que no se haya coloreado previamente. Comienza Alex. Cada uno quiere colorear, en total, la mayor cantidad posible de casillas. Si ambos juegan de la mejor manera posible, ¿cuántas casillas tendrán el color rojo? (Cuando Alex no puede jugar más, Fredy sigue hasta terminar el tablero.)
Segundo día
4. Sea O el punto de intersección de las
mediatrices de un triángulo ABC. Denotamos D al punto de
intersección de la recta AO con el segmento BC. Si
![]() ,
calcular la medida de los ángulos del triángulo.
,
calcular la medida de los ángulos del triángulo.
5. Un triángulo equilátero de lado 100 está dividido en 1002 = 10000 triángulos equiláteros de lado 1 mediante paralelas a sus lados. Decidir si es posible numerar los triángulos unitarios con los números de 1 a 10000, sin repetir números, de modo que el triángulo que tiene el número i tenga por lo menos un punto común con el triángulo que tiene el número i + 1 y por lo menos un punto en común con el triángulo que tiene el número i + 2 para todo i = 1, 2, ..., 9998.
6. Alrededor de una circunferencia hay escritos 53
dígitos distintos de cero. Hay que cortar la circunferencia en arcos de modo que
cada arco contenga al menos dos dígitos, y sumar los números que se hayan
formado de esta manera. (Todos los números se leen en el sentido de las agujas
del reloj.)
Demostrar que hay dos maneras diferentes de cortar la circunferencia para las
que las sumas obtenidas son iguales.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |