7mo
Torneo de Computación y Matemática
Tercera
Ronda
Capital Federal - 17 al 19 de diciembre de 2004
Primer día
Hallar todos los números enteros x entre 2 y 21 inclusive tal que x7-1 tenga menos de 9 divisores.
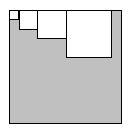
Javier toma un cuadrado de lado 2004, y va recortando cuadraditos de lado 1, lado 2, lado 3, etc., todos pegados al borde superior, hasta que ya no le entran más como muestra la figura. ¿Qué área queda sin recortar?

Considerar el siguiente enunciado:
"Un grupo de ciclistas recorrió 130?km a lo largo de
varios días. Los días soleados recorren 48km, y los que no lo
son, 2?km. ¿Cuántos días soleados hubo y cuántos días
les llevó en total?"
Llenar los ? para que el problema tenga solución única,
donde ? indica una cifra, no necesariamente la misma en
todos los casos.
Segundo día
Se tienen tres enteros positivos a, b, c
tales que:
a + b + c = 105
a2 + b2 + c2
= 4949.
Calcular todos los posibles valores de a3+b3+c3
.
Se quieren repartir 1000 pesos entre el primer, segundo y tercer puesto de un concurso. Los tres premios deben ser distintos, sin centavos, y obviamente el primero debe recibir más que el segundo, etc. ¿De cuántas formas distintas es posible hacer esto?
Decimos que un entero positivo es suave
si dos cifras consecutivas difieren en a lo sumo 1.
Por ejemplo: 12345, 33, 6, 121212, etc.
a) Hallar un primo suave mayor a 100000.
b) Contar cuántos primos entre 100000 y 1000000 son suaves.
Primer día
Harmann escribe los números enteros
positivos en un pizarrón suficientemente grande, de la siguiente
manera:
- en la fila 1, columna 1, escribe el número 1;
- luego, para cada número n = 2, 3, 4, ... en orden, lo
escribe en la primer fila que no contenga divisores de n,
en la primer columna libre.
Empieza así:
| fila | col 1 | col 2 | col 3 | ... |
| 1: | 1 | |||
| 2: | 2 | 3 | 5 | |
| 3: | 4 | 6 | ||
| ... |
a) Encontrar en que fila escribe el 2004
b) Encontrar en que fila escribe el 241001
c) Encontrar en que columna escribe el 2004
Dados cuatro números enteros a, b, c, d
y cuatro números enteros no negativos i, j, k, l se
define
p(x) = a · xi + b · xj + c · xk + d · xl
Por ejemplo si a=2, b=-3, c=10 y d=7 y i=4, j=0, k=2
y l=6 entonces
p(8)= 2 · 84 + (-3) · 80 + 10 · 82 + 7 · 86
= 1843837
Encontrar una posible elección de los valores de a, b, c, d,
i, j, k, l sabiendo que
p(1)= 16
p(2)= 240
p(5)= 81540
p(6)= 286896
Nota: el 0 es un entero no negativo, y x0
siempre vale 1, sin importar el valor de x.
Se definen los números pinchas de
la siguiente manera.
El 1 es pincha.
Un número entero mayor que 1 es pincha si y sólo si la suma de
los cuadrados de sus cifras es un número pincha menor.
¿Cuál es el mayor número pincha estrictamente menor a
1.000.000.000.000.000.000.000.000? (un cuatrillón, es decir, un
1 con 24 ceros atrás)
Segundo día
Un primo es siamés si y sólo si el número que se obtiene al dar vuelta sus cifras también es primo. Por ejemplo al dar vuelta las cifras de 87132 se obtiene 23178, que no son primos. Pero por ejemplo 13 es un primo siamés, de dos cifras. ¿Cuántos primos siameses de 5 cifras hay?
Brian pensó la siguiente sucesión:
1, 11, 21, 1211, 1231, 131221, 132231, 232221, 134211, 14131231,
etc.,
en este caso el primer término es 1, y a partir del segundo,
cada término se forma así: se cuenta las veces que aparece cada
cifra (9,8,7,...,1) en el término anterior, anotando la cantidad
de veces que dicha cifra aparece, seguida de la cifra. Por
ejemplo, en 134211 tenemos un cuatro, un tres, un dos y tres
unos, que forman 14131231. Si alguna cifra no está no se anota
nada, por ejemplo 12501->15122110.
Si se empieza por 102 tenemos otro ejemplo, que es: 102, 121110,
124110, etc.
a) Encontrar el término en la posición 2004, si el primer
término es 2009.
b) Hallar un valor para el primer término (o sea, X) de manera
que la sucesión sea de la forma X, Y, Z, X, Y, Z, ... con
X, Y y Z distintos.
a) ¿De cuántas maneras se pueden pintar
de blanco y de negro 7 puntitos en fila sin que haya tres juntos
(contiguos) de color negro?
b) ¿Y si son 14 puntitos?
c) ¿Y si son 21 puntitos?
d) ¿Y si son 28 puntitos?
Primer día
Uno de los momentos centrales del juego del
TEG es el combate. Consideremos algo que pasó una vez, China
ataca a Kamtchatka.
El atacante (China) usa 3 dados. El defensor (Kamtchatka) usa 2
dados. El atacante y el defensor tiran cada uno sus dados, y los
ordenan de mayor a menor por puntaje obtenido. Luego comparan los
dados, el mayor con el mayor, el siguiente con el siguiente,
etc., descartando el dado sin pareja.
Si cierto dado del atacante es estrictamente mayor que el
correspondiente dado del defensor, le corresponde un éxito al
atacante. Si fuera menor o igual, le corresponde un éxito al
defensor.
Ejemplo: China tira y obtiene 3,1,6; Kamtchatka 4,3. Se comparan
los dados:
China 6 vs Kamtchatka 4: éxito para China.
China 3 vs Kamtchatka 3: éxito para Kamtchatka.
El tercer dado de China se descarta.
Calcular la probabilidad de que China obtenga 2 éxitos.
Nota: la probabilidad es casos favorables / casos totales. Por
ejemplo con un dado cada uno, hay 15 casos favorables (6 vs 5, 6
vs 4, etc.) y 36 casos totales o posibles, entonces la
probabilidad es 15 / 36 ![]() 0.41666...
0.41666...
Todos los números de la forma x6-1,
con x entero estrictamente mayor que 3, tienen 16 o más
divisores positivos.
a) encontrar un ejemplo con exactamente 16 divisores
b) dar otro ejemplo con exactamente 16 divisores (distinto
del de a).
c) demostrar que efectivamente todos los números de la
forma x6-1, con x entero estrictamente
mayor que 3, tienen 16 o más divisores positivos.
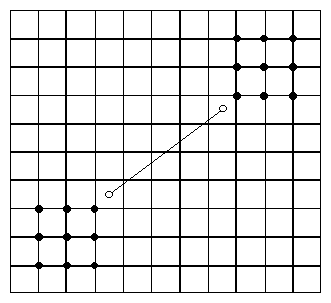
En un patio rectangular de 11x10 baldosas
cuadradas se marcan 9 intersecciones cerca de la esquina inferior
izquierda formando un cuadrado, y 9 intersecciones cerca de la
opuesta como se ve en la figura. Luego se unen con tiza las
primeras 9 intersecciones con las otras 9 intersecciones, todas
con todas, formando en total 81 segmentos.
Una hormiga camina desde el centro de la baldosa en la posición
(4,4) contando desde la esquina inferior izquierda, hasta el
centro de la baldosa (8,7) contando desde la misma esquina, como
se ve en la figura.
Sin tener en cuenta los segmentos de tiza que pasan por los
extremos del camino de la hormiga:
a) ¿Cuál es el primer segmento de tiza que pisa la hormiga en
su trayecto?
b) ¿Qué distancia recorre desde que empieza a caminar hasta
pisar este segmento?
Aclaración: Es posible que no haya intersección con algunos
segmentos.
Segundo día
Encontrar un número entero de 6 cifras ABCDEF,
todas distintas de cero, tal que
BCDEFA + DEFABC + EFABCD + FABCDE =
1386029
Se define el entrelazamiento de dos
enteros distintos a y b como el mayor entero positivo k tal que a
y b no son coprimos, a+1 y b+1 no son coprimos, a+2 y b+2 no son
coprimos, ..., a+(k-1) y b+(k-1) no son coprimos.
Por ejemplo, el entrelazamiento de 3 y 5 es 0, el de 4 y 14 es 3,
etc.
a) Hallar a y b distintos con máximo entrelazamiento si a y b
son menores que 1000.
b) Hallar a y b distintos con máximo entrelazamiento si a y b
son menores que 3000.
El Nim es un popular juego para dos jugadores, que tiene muchas variantes. En la que prefiere Pablo el "tablero" inicial consiste en 4 filas. Los jugadores juegan alternadamente por turnos. En su turno, un jugador elige una fila y tacha de ella una cierta cantidad de palitos, empezando desde la izquierda. Siempre se debe tachar al menos un palito. Los palitos tachados deben ser contiguos y estar todos en la misma fila (y estar pegados al extremo izquierdo). La figura muestra una partida posible.

Gana el jugador que tacha el último
palito, o sea que pierde el que ya no puede tachar ningún
palito.
a) Contar cuántas posibles partidas hay cuando el tablero
inicial es 1-2-3-4.
b) Contar cuántas posibles partidas hay cuando el tablero
inicial es 1-3-5-7.
Suponiendo que los dos jugadores son realmente muy astutos y
nunca se equivocan:
c) Decidir quién de los dos jugadores (el primero o el segundo)
gana la partida, por más que su oponente no se equivoque nunca,
cuando el tablero inicial es 1-2-3-4 .
d) Decidir quién de los dos jugadores (el primero o el segundo)
gana la partida, por más que su oponente no se equivoque nunca,
cuando el tablero inicial es 1-3-5-7.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |