Capital Federal, 14 al 16 de diciembre de 2005
Darío logró demostrar que la ecuación
y2 = x3 + 9
tiene diez soluciones enteras (o sea que x e y son números enteros). Encontrarlas a todas.
Contar cuántos números menores que 1000000, de la forma
8 · a2 · b - 6 · a2 + 4 · b2 + 5 · b - 6
con a y b enteros positivos, son primos.
Nota: Los números primos son los que tienen como únicos divisores al 1 y a sí mismos, por ejemplo 2, 3, 5, 7, 11, 13, ...
Un comerciante quiere fijar el precio de un producto, pero resulta que el producto tiene un 5% de impuesto sobre el precio base. Dado un precio base con dos decimales, se le suma el impuesto truncándolo a dos decimales.
Por ejemplo si el precio base es de $1.11 al agregarle el impuesto queda $1,1655 que se trunca a $1,16 y este último sería el precio al público.
Para comodidad de los clientes el precio final tiene que terminar en 00 centavos, es decir, ser entero. Por ejemplo, si el precio base es $2.86, el impuesto es $0.143, y el precio final es $3.00; por lo tanto $3 es un precio alcanzable.
Preguntas: ¿Hay algún precio final que no se pueda alcanzar? ¿Hay por lo menos tres precios finales que no se puedan alcanzar?
Para un interesante torneo, queremos armar un problema con la siguiente ecuación:
391 · x + 323 · y = n
Lo que buscamos es que si se calculan todos los posibles valores de x e y enteros positivos que cumplen con la ecuación con ese n, haya solución pero sea única (un solo valor posible de x e y).
a) Comprobar que se puede usar el valor n = 2006.
b) Si queremos que n esté entre 10000 y 100000, ¿qué valor de n podemos usar?
Calcular la suma de los divisores positivos impares de 87094528.
Nota: Por ejemplo los divisores de 33 son 1, 3, 11 y 33.
Cierto número de 5935 cifras está escrito usando sólo tres dígitos distintos, ninguno de los cuales aparece menos de 100 veces. La suma de sus cifras es 5981 y la suma de los cuadrados de sus cifras es 9957. ¿Qué dígitos son y cuántas veces aparece cada uno?
Ejemplo: 2005 tiene 4 cifras, la suma de sus cifras es 2+0+0+5 = 7, y la suma de los cuadrados de sus cifras es 4+0+0+25 = 29.
Encontrar todas las soluciones enteras positivas de
x2 + y3 +z4 = 20052005
Algunos números enteros positivos no se pueden escribir como suma de dos cuadrados perfectos (1, 4, 9, 16, 25, 36, etc.). Otros sí. Algunos se pueden escribir de varias formas distintas. Por ejemplo 50 = 1 + 49 = 25 + 25 se puede escribir de dos formas distintas. 1+49 es la misma forma que 49+1. Notar que 50 es múltiplo de 5.
a) ¿Cuántos enteros de 1 a 1000 se pueden escribir de 2 (dos) o más formas distintas como suma de dos cuadrados, pero no son múltiplos de 5?
b) ¿Cuántos enteros de 1 a 10000 se pueden escribir de 3 (tres) o más formas distintas como suma de dos cuadrados, pero no son múltiplos de 5?
c) ¿Cuántos enteros de 1 a 100000 se pueden escribir de 4 (cuatro) o más formas distintas como suma de dos cuadrados, pero no son múltiplos de 5?
Dados los enteros no negativos A, B y M, a partir de un término inicial x0 se construye la sucesión
xi+1 = (A · xi + B) mod M
donde mod es el resto de la división entera (16 mod 3 = 1, 6 mod 2 = 0, etc.)
Se buscan valores de M tales que
a) Encontrar dos valores de M que estén entre 10 y 100
b) Encontrar dos valores de M que estén entre 100 y 1000
Para cada uno de los cuatro valores de M encontrados, dar también un valor de A y B tales que se cumpla lo pedido.
Ejemplo 1: si A = 9, B = 2, y M = 12, una sucesión posible es x0 = 3, x1 = 5, x2 = 11, x3 = 5, ... En este caso no son todos distintos.
Ejemplo 2: si A = 1, B = 1, y M = 4, una sucesión posible es x0 = 0, x1 = 1, x2 = 2, x3 = 3, (x4 = 0) En este caso 4 · ( x0 · x1 + x1 · x2 + x2 · x3 + x3 · x4) = 4(0 + 2 + 6 + 0) = 32, mientras que M · (M-1)2 = 36, así que no se cumple la tercera condición.
Una calculadora muestra cada número utilizando 7 segmentos, como se muestra en la figura:
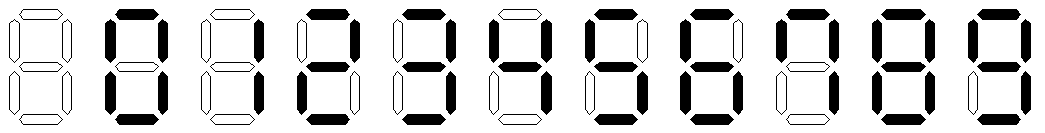
Por ejemplo para mostrar el número 8 prende los 7 segmentos, en cambio para mostrar el número 3 utiliza sólo 5 segmentos.
Encontrar un número que sea múltiplo de 107 y que para mostrarlo se tengan que utilizar exactamente 16 segmentos
Agustín quiere llenar el siguiente tablero de 4x4 con números enteros distintos de manera que el número que está en cada casilla sea un múltiplo del número que está en la casilla que está a su izquierda y de la casilla que está abajo. Y además se quiere que en la esquina inferior izquierda esté el número 1, en la esquina superior derecha este el número 192433829.

Se tienen tiras de caritas en fila. Algunas están bien y otras están al revés. Una carita del medio es feliz si alguna de sus dos vecinas mira para el mismo lado. Una carita de la punta es feliz si su única vecina mira para el mismo lado.
![]()
En el ejemplo de la figura hay 5 caritas felices: 2 bien y 3 al revés.
a) Consideramos todas las posibles filas que tienen 5 caritas para arriba y 5 para abajo. ¿Cuál es el promedio de caritas felices?
b) ¿Y si consideramos las filas con 10 y 10 caritas?
Consideramos el número N = 2005!, y el número K que es la cantidad de divisores positivos de N.
a) Calcular la cantidad de cifras de N.
b) Calcular la cantidad de cifras de K.
Aclaración: m!=1·2·3·...·mes el factorial de m, por ejemplo 4! = 24, que tiene 2 cifras. Además que tiene 8 divisores: 1, 2, 3, 4, 6, 8, 12 y 24. La cantidad de cifras de 8 es 1.
Para reactivar la economía, el ministerio de economía decide emitir monedas de 1 centavo, 2 centavos, 3 centavos,..., 99 centavos.
a) ¿Cuál es la menor cantidad de monedas que hay que llevar en el bolsillo, sin repetir valores, para estar seguro de poder pagar exactamente todos los precios de 1 a 99 centavos?
Hay muchas formas distintas de elegir esta cantidad mínima de monedas.
b) ¿De cuántas maneras distintas se pueden elegir esas monedas?
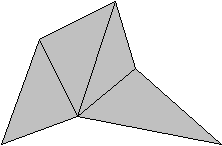
Federico compró 9 maderitas de largo 18, 19, ... ,25 y 26. Con estas maderitas armó un abanico uniendo las maderitas por las puntas, de manera que las maderitas eran los lados de un polígono y todas las diagonales correspondientes a un punto. Determinar la disposición en que deben colocarase las maderitas para que la superficie del abanico sea máxima.
Analizamos las siguientes cuatro ecuaciones:
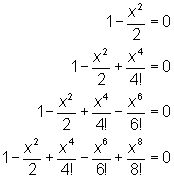
Solamente nos interesa considerar la solución que cada una de ellas tiene entre 1 y 3.
a) Calcular la solución exacta de las dos primeras
b) Aproximar la solución de cada una con un error menor que 10-5
Aclaración: m!=1·2·3·...·m es el factorial de m, por ejemplo 4! = 24.
a) Sea N = 200520052005 ¿Cuántas veces aparece el dígito 1 en su escritura en base 3?
b) Sea M = 200520052005…20052005, el número (escrito en base 10) que se obtiene al escribir 708 veces el 2005. ¿Cuántas veces aparece el dígito 1 en su escritura en base 3?
Ejemplo 1: 9876543210 (en base 10) = 221111022110101020200 (en base 3).
Ejemplo 2: el número que se obtiene al escribir dos veces el 2005 es 20052005 (en base 10) = 1101201202011212 (en base 3).
Se tiene un tablero cuadrado de 4x4. Dos casillas son vecinas si tienen un lado en común, así que cada casilla tiene 2, 3 o 4 vecinas.
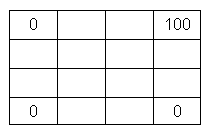
En tres de las esquinas se escribe el número 0 y en la otra se escribe el número 100. Se quiere completar el resto del tablero con números enteros, de manera que la diferencia entre el valor puesto en cada casilla y el valor del promedio de sus vecinas sea chica.
Encontrar una manera de completarlo tal que la diferencia en cada casilla, salvo las cuatro esquinas, sea ...
a) ... menor o igual a 10.
b) ... menor o igual a 2.
c) ... menor o igual a 1.
|
|
Olimpíada Matemática
Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |