Muestra cómo cortar el rectángulo en la menor cantidad posible de piezas, y arma el cuadrado.
XI Olimpíada
Matemática Rioplatense
Diciembre de 2002.
| nivel A |
Versión en Español
1. Encuentra todos los números de dos cifras que son múltiplos de la suma de sus cifras.
2.
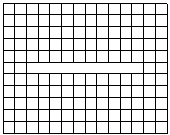
De una hoja cuadriculada rectangular de 11x 14 se recortó un rectángulo
central de 1 x 10, como muestra la figura. Se quiere cortar la hoja siguiendo
las líneas de la cuadrícula de manera que con todas las piezas obtenidas se
pueda armar un cuadrado, sin huecos ni superposiciones
Muestra cómo cortar el rectángulo en la menor cantidad posible de piezas,
y arma el cuadrado.
3.
Doce personas están sentadas alrededor de
una mesa redonda, numeradas del 1 al 12 en forma consecutiva. En el primer
turno, la persona número 1 entrega una cantidad de dinero igual a 
de
lo que tiene en ese momento a cada una de las dos personas que le siguen (la número
2 y la número 3). Este proceso se repite con cada persona de la mesa: cada uno
en su turno le da una cantidad de dinero igual a 
de
lo que tiene en ese momento a cada una de las dos personas que le siguen. En el
penúltimo turno, la persona número 11 les da dinero a la número 12 y a la número
1. En el último turno, la persona número 12 les da dinero a la número 1 y a
la número 2. Al final, las 12 personas tienen exactamente $100 cada una.
Determina qué cantidad de dinero tenía cada persona antes de comenzar el primer turno.
Versión en Español
4. Daniel tiene una balanza de dos platillos y 10 piedras cuyos pesos son todos los números enteros entre 1 y 10 (inclusive). Él quiere colocar algunas piedras en la balanza de tal forma que los platillos se equilibren.
(a) Determina cuál es el mayor número de piedras que puede colocar. Justifica por qué es el mayor y muestra un ejemplo.
(b) Determina cuál es el mayor número de piedras que puede colocar si en cada platillo debe haber la misma cantidad de piedras. Justifica por qué es el mayor y muestra un ejemplo.
5.Si se escribe un número en una hoja de papel y se gira la hoja 180º, los dígitos 0, l y 8 no cambian (se siguen leyendo 0, l y 8, respectivamente); el 6 se lee 9 y el 9 se lee 6. Los demás dígitos dejan de tener significado. Un número se dice giratorio si cuando se lo escribe en una hoja de papel, se lee el mismo número antes y después de girar la hoja 180º.
Calcula la suma de todos los números giratorios de 7 cifras.
6.Tenemos 2002 monedas formando una circunferencia, algunas con la cara (C) hacia arriba y otras con la cruz (K) hacia arriba. Se realiza la siguiente operación: se elige una moneda con la cara C hacia arriba y se dan vuelta las dos monedas vecinas.
¿Es posible que después de realizar la operación varias veces solamente quede una moneda con la cara C hacia arriba si al principio:
(a) había 2000 monedas que tenían la cara (C) hacia arriba?
(b) había 2001 monedas que tenían la cara (C) hacia arriba?
En ambos casos, si la respuesta es no, justifica por qué, y si la respuesta es sí, muestra cómo hacerlo.
| nivel 1 |
Versión en Español
1. Tenemos un tablero cuadrado de 2002 x 2002 con casillas pintadas de negro y blanco, como un tablero de ajedrez. Las filas han sido numeradas del 1 al 2002 y las columnas del 1 al 2002 (la casilla en la fila 1 y la columna 1 es negra). En cada casilla escribimos el producto del número de la fila por el número de la columna a las que la casilla pertenece. Sean A la suma de los números escritos en las casillas negras y B la suma de los números escritos en las casillas blancas.
Demuestra que A – B es un cuadrado perfecto.
2.
Sean ABCD un rectángulo con AB > BC, y O el punto de intersección de sus
diagonales AC y BD. La bisectriz del ángulo 
corta
a BD en E. Llamamos M al punto medio de AB. Se traza por E la perpendicular a
AB, que corta a AB en F; se traza por E la perpendicular a AE, que corta a AC en
H. Si es dado que 
y 
,
calcula el área del rectángulo ABCD en términos de a.
3.
Una pista para carreras de automóviles consiste de 6 circunferencias 
,
, 
,
, 
y
,
tangentes interiores en un punto P. Las longitudes de las circunferencias son 1
km, 2 km, 4 km, 8 km, 16 km y
32 km, respectivamente. Dos pilotos, A y B, viajan a lo largo de la pista del
siguiente modo: comenzando en el punto P, el piloto A recorre 
,
cuando llega de nuevo a P recorre 
,
luego recorre 
,
hasta que completa todo el recorrido de la pista y llega de nuevo a P. Allí
comienza todo el recorrido nuevamente, una y otra vez. Viaja todo el tiempo a
velocidad constante, y recorre cada una de las circunferencias en el mismo
sentido. El piloto B inicia su viaje algo más tarde que A, y recorre las
circunferencias 
,
, 
,
, 
y
en
el mismo orden que lo hace A, a la misma velocidad que A, pero lo hace siempre
en sentido contrario al de A.
Supongamos que B conoce la hora a la que A inició su recorrido. Decide si B puede elegir la hora de inicio de su propio recorrido de modo tal que los dos automóviles no se crucen nunca en la pista.
Versión en Español
4. Se tienen 2 cuadriláteros convexos iguales de papel: ABCD y A'B'C'D' (AB = A'B'; BC = B'C'; CD = C'D'; DA = D'A'). Se corta el cuadrilátero ABCD por la diagonal AC y se corta el cuadrilátero A'B'C'D' por la diagonal B'D', obteniendo así cuatro trozos de papel.
(a) Indica un procedimiento, que no dependa de la forma particular del cuadrilátero convexo ABCD, que permita armar un paralelogramo con los cuatro pedazos de papel, sin huecos ni superposiciones.
(b)Si los lados de los cuadriláteros miden 3, 3, 4 y 6, demuestra que se puede armar un paralelogramo tal que su perímetro sea mayor que 16 y menor que 28, cualquiera sea el orden de los lados.
5. Se dispone de una hoja cuadriculada. Diremos que una línea quebrada cerrada formada por segmentos que están sobre las rectas de la cuadrícula es especial si no hay dos segmentos que estén sobre una misma recta de la cuadrícula.
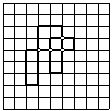
En la figura se muestra una línea especial con 10 segmentos y 4 puntos de cruce.
Dibuja una línea especial con exactamente 22 segmentos que tenga el máximo número posible de puntos de cruce. Explica por qué es imposible que el número de puntos de cruce sea más grande que el hallado.
6. Cintia tiene una larga tira de papel donde están escritos todos los números naturales de 20 dígitos, ordenados de menor a mayor (desde 100…00 hasta 999…99) sin espacios entre números consecutivos. Cintia elige un número entero positivo k y se lo dice a Elicita. A continuación Elicita elige k dígitos consecutivos de la tira de papel, hace una fotocopia del segmento de papel que contiene esos k dígitos y se lo entrega a Cintia. Con esta tira de k dígitos a la vista, Cintia debe determinar el lugar exacto de la tira larga de papel donde se encuentra el segmento fotocopiado.
Halla el menor valor de k que le permite a Cintia cumplir el objetivo, no importa cuáles sean los k dígitos consecutivos que decida fotocopiar Elicita.
| nivel 2 |
Versión en Español
1.
Sean a, b y c números reales positivos. Demostrar que 
.
2. Sea A un subconjunto del conjunto N de los números enteros positivos. Diremos que un subconjunto B de N es una base de A si las sumas de los elementos de cada subconjunto no vacío de B son distintas y cada elemento de A es igual a una de estas sumas. Demostrar que para cada n = 1, 2, 3,… existe un k(n) tal que cada subconjunto de N con n elementos tiene una base con a lo sumo k(n) elementos, y determinar (para cada n) el valor mínimo de k(n).
3.
Sea ABC un triángulo tal que el ángulo 
.
Sean P y Q puntos interiores del triángulo ABC tales que 
y
.
Sean D y E los pies de las perpendiculares trazadas desde P a los lados CA y AB,
respectivamente. Demostrar que Q es el ortocentro del triángulo ADE.
Versión en Español
4.
Decidir si es posible colocar 99 cuadrados de 3 ´ 3 en un tablero de 48 ´ 48
de modo que cada cuadrado cubra exactamente 9 casillas del tablero y que no
quede lugar en el tablero para colocar otro cuadrado de
3 ´ 3 que cubra exactamente 9 casillas del tablero y que no se superponga con
ninguno de los 99 ya colocados.
5. Dado un cuadrilátero ABCD se construyen triángulos isósceles ABK, BCL, CDM y DAN, cuyas bases son los lados AB, BC, CD y DA, y tales que K, L, M y N son puntos distintos y no hay tres de ellos alineados. La perpendicular a la recta KL trazada por B corta a la perpendicular a la recta LM trazada por C en el punto P; la perpendicular a la recta MN trazada por D corta a la perpendicular a la recta NK trazada por A en el punto Q. Demostrar que, si P y Q son puntos distintos, entonces PQ es perpendicular a KM.
6.
Sean 
números
enteros tales que existen infinitos enteros positivos k con 
para
algún i.
Demostrar
que para cada entero positivo n, existe un entero positivo j tal que 
.
| nivel 3 |
Versión en Español
1. Determinar todos los pares (a, b) de enteros positivos para los cuales
es un número entero.
2.
Sea l un número real tal que la desigualdad 
se verifica para infinitos pares (a, b) de números enteros positivos.
Demostrar que l ³ 5.
3.
Sea ABC un triángulo con 
.
El punto P es el simétrico de A respecto del punto de tangencia de la
circunferencia inscrita con el lado BC. Demostrar que si la mediatriz del
segmento CP corta a la recta que contiene a la bisectriz del ángulo 
en
el punto Q, entonces el triángulo CPQ es equilátero.
Versión en Español
4. Sean a, b y c números reales positivos. Demostrar que
.
5. Sean G la circunferencia circunscrita y O el circuncentro de un triángulo ABC con AC ¹ BC. La recta tangente a G trazada por C corta a la recta AB en M. La recta perpendicular a OM trazada por M corta a las rectas BC y AC en P y Q, respectivamente. Demostrar que los segmentos PM y MQ son iguales.
6. Daniel elige un entero positivo n y se lo dice a Ana. Con esta información, Ana elige un entero positivo k y se lo dice a Daniel. Daniel traza n circunferencias en un papel y elige k puntos distintos con la condición de que cada uno de ellos pertenezca a alguna de las circunferencias que trazó. Luego borra las circunferencias, y sólo quedan visibles los k puntos que marcó. A partir de estos puntos, Ana debe reconstruir por lo menos una de las circunferencias que trazó Daniel. Determinar cuál es el menor valor de k que le permite a Ana lograr su objetivo independientemente de cómo elija Daniel las n circunferencias y los k puntos.
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |