XIX Olimpíada
Matemática Rioplatense
Diciembre de 2010
| Nivel A |
1. 2010 fósforos se disponen en escalera como se indica en la siguiente figura:
a) ¿Cuál es el número de la escalera que contiene al último fósforo?
b) ¿En qué nivel está la cabeza de ese último fósforo?
2.
Se tienen 2010 tarjetas numeradas del 1 al 2010. Se eligen todas las tarjetas
que tienen escrito un número cuya suma de dígitos es impar. Hallar la suma de
todos los números escritos en las tarjetas elegidas.
Nota: en el número 724 los dígitos son 7, 2 y 4, y la suma de los dígitos es
7+2+4 = 13
3. Una hoja rectangular cuadriculada con 59×133 cuadraditos se quiere partir en la mayor cantidad posible de trozos rectangulares mediante dos cortes. Antes de cortar está permitido doblar la hoja a lo largo de líneas de la cuadrícula todas las veces que sea necesario. Luego se apoya la hoja doblada sobre la mesa y se hacen dos cortes rectos a lo largo de líneas de la cuadrícula que hayan quedado visibles después de los dobleces. Los dos cortes deben ir de lado a lado de la hoja doblada. ¿Cuál es el máximo número de trozos que se pueden obtener de este modo? Explicar cómo se hacen los dobleces y los cortes.
4. Bibi escribió un número natural. Si se suman todos los números naturales menores que el número que escribió Bibi, se obtiene un número de tres cifras iguales. Determinar qué números pudo haber escrito Bibi.
5. Un cubo de arista 10 se corta con tres pares de planos paralelos a las caras, y queda dividido en 27 paralelepípedos. Las aristas del paralelepípedo interior miden 1, 2 y 3; además de esto, no se sabe nada acerca de la ubicación de los cortes. Hallar la suma de los volúmenes de los 8 paralelepípedos de las esquinas del cubo.
6.
En cierto país sólo hay monedas de 11 pesos y de 13 pesos (no hay billetes). En
una heladería que está por abrir hay una fila de clientes esperando. Cada
cliente quiere comprar un helado y tiene exactamente 155 pesos. El helado cuesta
12 pesos. El heladero quiere atender a todos utilizando sólo el dinero que tiene
en la caja. Al pagar cada cliente le entrega los 155 pesos, el heladero se cobra
los 12 pesos y le devuelve al cliente la diferencia. Para iniciar las ventas, el
heladero le pide al dueño de la heladería cierta suma de dinero, y sabe que éste
le dará alguna suma mayor a la pedida.
¿Cuál es el mínimo monto de dinero que el heladero debe pedir al dueño para
poder realizar las ventas sin importar el monto que el dueño le entregue?
| Nivel 1 |
1. Se
considera una semicircunferencia de diámetro AB, centro O y radio
.
Sea C el punto del segmento AB tal que AC =
.
La recta l es perpendicular a AB por C y D es el
punto de intersección de l y la semicircunferencia. Sean H el pie
de la perpendicular trazada desde O hacia AD y E el punto
de intersección de las rectas CD y OH.
a)
Calcular AD en función de .
b) Si M y N son los puntos medios de AE y OD respectivamente, hallar la medida del ángulo MHN.
2. En cada casilla de un tablero rectangular de 4 filas y n columnas está escrito uno de los números 1, 2 ó 3. Para cualesquiera tres columnas distintas hay una fila que corta a dichas columnas en tres casillas que contienen tres números distintos. Hallar el máximo n para el cual existe tal tablero.
3.
Hay 2k cajas (k 
2)
con 2k – 1 piedras en cada una. Una movida legal es elegir 2k – 2
cajas y quitarle una piedra a cada una de ellas. Los jugadores A y B juegan
alternadamente; comienza A. Un jugador gana si en una de sus jugadas logra
vaciar dos cajas. Determinar qué jugador tiene estrategia ganadora y describir
dicha estrategia.
Segundo Día
4. Decimos que un número entero x (1 ≤ x ≤ 100) es miembro de la familia n si x tiene exactamente n divisores positivos. Por ejemplo, 12 es miembro de la familia 6 pues tiene 6 divisores positivos: 1, 2, 3, 4, 6 y 12. ¿Cuál es la familia que tiene la mayor cantidad de miembros?
5. Consideremos la siguiente secuencia de tableros
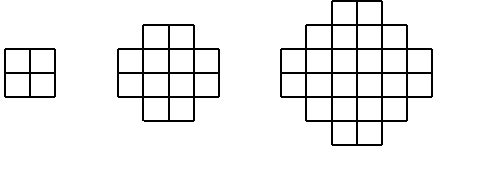
En cada casilla de un k – tablero hay un botón y un foco. Inicialmente
todos los focos están apagados. Cada vez que se presiona un botón cambian de
estado (de apagado a encendido o de encendido a apagado) solamente los focos
ubicados en las casillas vecinas a la casilla del botón presionado. Para cada
valor de k, determinar el máximo número de focos que pueden quedar
encendidos en el k - tablero después de presionar algunos botones.
NOTA: Dos casillas son vecinas si tienen un lado en común.
6. Se
tienen dos números A y B, cada uno de 100 dígitos, formados exclusivamente por
dígitos 4 y 7. La suma A + B tiene 101 dígitos, de los cuales exactamente 20 son
4 y exactamente 30 son 9.
Determinar la cantidad de dígitos 1 que puede tener A + B.
| Nivel 2 |
1. Calcular la suma
.
ACLARACIÓN:
indica
el mayor entero menor o igual que x.
2. En el paralelogramo ABCD se ubica G en el lado AB. Se considera la circunferencia que pasa por A y G y es tangente a la prolongación de CB en un punto P. La prolongación de DG interseca a la circunferencia en L. Si el cuadrilátero GLBC es cíclico, demostrar que AB = PC.
3. Sea N ³ 4 un entero fijo. Dos jugadores, A y B, escriben números en el pizarrón, un número a continuación del otro, con las siguientes reglas: A escribe +1 o -1; luego B escribe +2 o -2; en la jugada siguiente A escribe +3 o -3 y así sucesivamente, en la jugada k, el jugador que tiene el turno escribe +k o -k. El objetivo de cada uno es que al cabo de una de sus jugadas la suma de algunos términos consecutivos de la expresión obtenida, tomados con sus signos, sea divisible por N. Para cada N determinar cuál de los dos jugadores tiene estrategia ganadora, si es que hay alguno.
Versión en Español
4. Hay 1000 puntos distintos sobre una circunferencia. Tenemos que seleccionar k de ellos de modo que no haya entre los elegidos dos adyacentes. ¿De cuántas maneras se puede hacer?
5. En una hoja infinita de papel cuadriculado se han coloreado 999 cuadraditos de negro. Llamamos especial a un rectángulo con lados en la cuadrícula si tiene dos casillas negras en esquinas opuestas (se consideran también los rectángulos con uno de sus lados igual a 1). Sea N el máximo número de cuadraditos negros dentro de un rectángulo especial para una configuración dada. Hallar el mínimo de N sobre todas las configuraciones.
6.
Sea n un entero positivo. Diremos que una sucesión de números enteros
,
con 
,
es suave si existe un entero m, con
<
k, tal que 
,
,
…, 
.
Además, diremos que la sucesión es universal si cada una de las
sucesiones que se obtienen al reemplazar
por
cada uno de los números 1, 2, …, n es suave. Para cada n hallar
una sucesión universal de longitud mínima.
| Nivel 3 |
1. Sean
a, b, c y d enteros positivos distintos tales que
divide
a 
,
divide
a 
y
divide
a 
.
a) ¿Es posible decidir cuál de los números a, b, c, d es el menor?
b) ¿Es posible decidir cuál de los números a, b, c, d es el mayor?
2.
En el triángulo acutángulo ABP (AB mayor que BP) se trazan
las alturas BH, PQ y AS. La prolongación de QS corta
a la recta AP en C. La prolongación de HS corta a BC
en L. Si HS = SL y HL es perpendicular a BC,
calcular 
.
3.
Hallar todas las funciones 
que
satisfacen la ecuación
para todos
tales
que 
.
ACLARACIÓN:
es
el conjunto de los enteros positivos.
4. Sean r1, r2, ..., r1000 los restos de la división de un entero positivo impar por 2, 3, …, 1000. Se sabe que los restos son distintos dos a dos y uno de ellos es 0. Hallar todos los valores de k para los cuales es posible que rk = 0.
5.
Hallar el mínimo y el máximo de la suma
donde
a, b, c, d son enteros positivos que satisfacen a
+ c = 20202, b + d = 20200.
6. Dos jugadores A y B juegan el siguiente juego. Inicialmente A ordena a su elección los números 1, 2, …, n en una fila; n es un entero positivo dado. A continuación, B elige un número y coloca una piedra sobre él. Luego A mueve la piedra a un número adyacente, luego B hace lo mismo, y así siguiendo. La piedra puede colocarse sobre el número k a lo sumo k veces, k = 1, …, n; la movida inicial de B se cuenta. El que no puede mover, pierde. Determinar, para cada n, quién tiene estrategia ganadora.
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |