VIII Olimpíada Matemática Rioplatense
6 al 10 de Diciembre de 1999

1

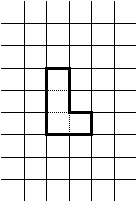
Un polígono se dice legal si sus vértices están sobre una cuadrícula y cada uno de sus lados es horizontal o vertical. La distancia entre dos puntos vecinos de l a cuadrícula es de 1cm. Por ejemplo, el polígono de la siguiente figura es legal.

1. ¿Habrá un polígono legal con perímetro igual a 22cm y área igual a 14cm²? En caso afirmativo, muestra un ejemplo y en caso contrario, explica por qué no.
2. ¿Habrá un polígono legal con perímetro igual a 21cm y área igual a 14cm²? En caso afirmativo, muestra un ejemplo y en caso contrario, explica por qué no.

2

Ana va a hacer fichas cuadradas de cartulina. Una cara la va a dividir en cuatro partes iguales como muestra la figura.

Cada una de las cuatro partes de cada ficha que haga la va a pintar de un color. Para ello dispone de 7 colores, los cuales puede repetir en una misma ficha o en fichas distintas. ¿Cuántas fichas distintas puede hacer?

Nota: dos fichas se consideran iguales si una se puede obtener de la otra girando. Por ejemplo, son iguales las siguientes fichas:

 

R	A
V	A

3

En cierta ciudad hay sólo dos clases de habitantes, los honestos, que siempre dicen la verdad y los mentirosos, que siempre mienten. Un viajero llega a esta ciudad y se encuentra con cuatro habitantes, A, B, C, D.

El habitante A le dice: "Exactamente uno de nosotros cuatro es mentiroso.".

El habitante B dice: "Nosotros cuatro somos mentirosos.".

A continuación el viajero le preguntó a C: "¿Es A mentiroso?". Recibió una respuesta (sí o no) de la que le resultó imposible saber qué clase de habitante era A.

Determina si D es honesto o mentiroso y justifica tu respuesta.

4

Están 2000 niños formando una fila y van a jugar a decir cada uno un número de la siguiente forma: el primer niño dice 1, el segundo dice dos más que el primero, o sea dice 3, el tercero, tres más que el anterior, o sea 6, el cuarto, dos más que el anterior, dice 8, el quinto, tres más que el anterior, dice 11 y así sucesivamente.

1. ¿Qué número dice el niño que está en el lugar 1999?
2. ¿Algún niño dice el número 1999?

Si tu respuesta es sí, indica en qué lugar de la fila está ese niño.

Si tu respuesta es no, indica en qué lugar de la fila están los niños que dicen los dos números más cercanos a 1999.

5

El entrenador del equipo de natación decidió organizar una serie de prácticas ente los siete integrantes del equipo. Cada día se hará una sola competencia en la que participarán tres de ellos. Cada nadador competirá sólo una vez con cada uno de los restantes.

1. ¿Cuántos días durará esta serie de prácticas? Explica por qué no puede durar ni más, ni menos días de los que dices.
2. Muestra una posible distribución indicando los tres nadadores que compiten cada día.

6

Se dice que un número entero positivo es bueno si entre sus dígitos no tiene el 0, ni el 1. Por ejemplo, 2326 es bueno y los números 2145, 3070 y 107 no son buenos.

Para cada número bueno entre 1 y 9919, considera el producto de sus dígitos. Por ejemplo, el producto de los dígitos de 2326 es 2 . 3 . 2 . 6 = 72 y para los números de un solo dígito, considera que el producto de sus dígitos es igual al mismo número.

Calcula la suma de todos estos productos.

1

Se tienen 1000 paquetes y cada uno de ellos contiene 4 fichas: tres fichas marcadas con un 9, y una ficha con un 1.

1. Escribir un número que sea múltiplo de 99 usando todas las fichas de una cierta cantidad de paquetes, distribuyendo los 1 los 9 adecuadamente.
2. ¿Cuál es el menor número natural que se puede formar de tal manera que se cumplan las condiciones dadas en a?

2

Sea AB un segmento con punto medio M. Sobre la mediatriz de AB se toma un punto O tal que OM = AM. Sea C una circunferencia de centro O y radio menor que OM. Por A se traza la recta AP tangente a C en P y que no corta al segmento OM. Por B se traza la recta BQ tangente a C en Q y que corta al segmento OM. Demostrar que AP y BQ son perpendiculares.

3

En un torneo de fútbol cada equipo juega exactamente un partido contra cada uno de los restantes. El ganador recibe 3 puntos y el perdedor 0 puntos, en caso de empate cada equipo recibe 1 punto. Diremos que el torneo es ilógico si finalizado el torneo, hay un equipo que ganó menos partidos que cada uno de los demás equipos, pero obtuvo más puntos que cada uno de los demás equipos. Determinar todos lo valores posibles para el número de equipos que puede haber en un torneo de fútbol ilógico.

(Faltan los problemas 4, 5 y 6)

1

Considere dos puntos A y B en el plano y l una recta tal que A y B se encuentran en un mismo semiplano determinado por l. Sean C tal que A y C son simétricos con respecto a la recta l, D el pie de la perpendicular de B a l, y s la mediatriz de BC. La circunferencia de diámetro BC intersecta a s en E y F. Sean G y H las intersecciones de l con los segmentos CE y CF, respectivamente. Demuestre que se cumple la siguiente relación entre las medidas de los ángulos:

AGC = 2 BGE y AHC = 2 BHF

2

Hallar todos los enteros n, n > 1, tales que cada divisor primo de n⁶ - 1 es divisor de n² -  1 o de n³ - 1

3

En un torneo de ajedrez cada jugador enfrenta exactamente una vez a cada uno de los restantes, y recibe 1, ½ o 0 puntos por una victoria, un empate o una derrota, respectivamente. Diremos que un torneo de ajedrez fue lógico si, una vez finalizado, para cada pareja de participantes A y B, tales que A ganó el partido contra B, se verifica que el puntaje final de A es mayor que el puntaje final de B. Definimos el resultado de un torneo como la sucesión de los puntajes finales obtenidos por cada uno de los participantes, ordenados de mayor a menor (pueden haber puntajes repetidos).

Demuestre que el resultado de cualquier torneo es también el resultado de algún torno lógico.

4

Cada noche tres personas de un grupo de n personas salen a cenar juntas. Después de cierto período de tiempo se observa que cada par de personas han cenado juntas exactamente una vez. Demuestre que n deja un resultado de 1 o de 3 al dividirlo por 6.

5

Sean ABC un triángulo y D, E y F puntos sobre los lados BC, CA y AB, respectivamente. Sean D’, E’ y F’ los puntos simétricos a D, E y F con respecto de los puntos medios de BC, CA y AB, respectivamente. Demuestre que si el triángulo DEF es congruente al triángulo D’E’F’ y los siguientes ángulos son iguales: D = D’, E = E’ y F = F’, entonces el triángulo DEF es semejante al triángulo ABC.

6

Se divide un cuadrado de lado 1 en dos partes, mediante una línea recta. Después, una de esas dos partes se divide en dos partes mediante otra línea recta, y quedan en total tres pedazos. Así siguiendo, en cada paso se toma un pedazo y se le divide en dos, mediante una línea recta. Después de 1999 de estas divisiones, el cuadrado queda dividido en 2000 pedazos. Demuestre que entre los 2000 pedazos existe por lo menos uno que puede cubrir totalmente un cuadrado de lado 1/2000.

1

Sea ABC un triángulo acutángulo escaleno cuyo ortocentro es H. M es el punto medio del segmento BC. N es el punto donde se intersectan el segmento AM y la circunferencia determinada por B, C y H. Demuestre que las rectas HN y AM son perpendiculares.

2

Sean k primos distintos p₁, p₂, ..., p_k. Consideramos todos los enteros positivos que sólo usan estos primos (no necesariamente todos) en su descomposición en factores primos, y ordenamos esos números en orden creciente, formando una sucesión infinita:

a_l < a₂ < ... < a_n < ...

Demuestre que, para cada número c, existe n tal que a_n+1 - a_n > c.

3

Dos jugadores A y B disputan el siguiente juego: A elige un punto, de coordenadas enteras, del plano y lo colorea de verde; luego B elige 10 puntos de coordenadas enteras, aún no coloreados, y los colorea de amarillo. El juego continúa siempre con las mismas reglas; A y B eligen uno y diez puntos no coloreados y los colorean de verde y amarillo, respectivamente.

a. El objetivo de A es lograr 111² puntos verdes que sean las intersecciones de 111 rectas horizontales y 111 rectas verticales (paralelas a los ejes coordenadas). El objetivo de B es impedírselo. Determine cual de los dos jugadores tiene una estrategia que le asegure lograr su objetivo.

b. El objetivo de A es lograr 4 puntos verdes que sean los vértices de un cuadrado de lados paralelos a los ejes coordenadas. El objetivo de B es impedírselo. Determine cuál de los dos jugadores tiene una estrategia que le asegure lograr su objetivo.

(Faltan los problemas 4, 5 y 6)

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar