IX Olimpíada
Matemática Rioplatense
11 al 15
de Diciembre de 2000
| nivel A |
1
Las posibles calificaciones para un examen eran 0, 1, 2, 3, 4. Después de la corrección se observó que el número de estudiantes que obtuvieron 3 puntos fue igual al número de estudiantes que obtuvieron 2 puntos. Además, todos consiguieron por lo menos 1 punto. La suma de todos los puntos obtenidos por los estudiantes en el examen fue igual al número de estudiantes aumentado en 30. Encuentra el número de estudiantes que consiguieron por lo menos 3 puntos.
2
Cuatro equipos A, B, C y D disputan un torneo de fútbol. Todos juegan contra todos (una única vez). En caso de victoria, el equipo ganador obtiene 3 puntos y el perdedor 0 (cero) puntos. Si hay empate, cada equipo obtiene 1 punto.
Al final del torneo, los puntajes de los equipos A, B, C, D fueron a, b, c, d, respectivamente.
Se observó que a < b < c < d, y b - a = c - b = d - c.
Encuentra todas las posibles puntuaciones finales de los 4 equipos. Para cada una de esas posibilidades construye una tabla con los resultados de los juegos y justifica por qué estas son las únicas puntuaciones posibles.
Por ejemplo: Una puntuación final posible es: a = 3, b = 3, c = 3, d = 3 y la tabla es:
| A empata con B | B empata con C | |
| A empata con C | B empata con D | |
| A empata con D | C empata con D |
3
Cierto país tiene solamente monedas de 1, 2, 3 y 4 centavos, y la entrada al zoológico cuesta 1 centavo. Un grupo de personas se dice afortunado si ningún integrante del grupo tiene monedas de 1 centavo, pero todos tienen monedas de mayor valor, y cuando juntan todas sus monedas pueden pagar sus entradas y cada miembro del grupo recibe el cambio exacto, utilizando solamente monedas de los otros miembros del grupo (sin pedirle al cajero, ni pedir prestado). Un ejemplo de un grupo afortunado es uno de dos personas, una con dos monedas de 2 centavos y la otra con una moneda de 3 centavos. Juntan las tres monedas, pagan las entradas con una moneda de 2 centavos y con las dos monedas restantes reciben su vuelto de 3 centavos y 2 centavos, respectivamente.
Determina el mínimo número de monedas que puede tener, en conjunto, un grupo afortunado de 15 personas y muestra cómo se pueden distribuir estas monedas entre las 15 personas.
4
Una "palabra" es una secuencia de letras. Consideramos las siguientes operaciones:
Por ejemplo, si la palabra inicial es ABCD, podernos hacer:
ABCD --> ABC --> ABCABC --> BCABC --> CABC --> CABCCABC
a) Muestra una secuencia de estas operaciones que transforme la palabra ABC en la palabra CBA.
b) Muestra una secuencia de estas operaciones que transforme la palabra ABCDE en la palabra EDCBA.
5
Patricia marcó varios puntos sobre una circunferencia. Después trazó algunos segmentos con extremos en esos puntos.
Al finalizar observó que en su figura cada punto era extremo de por lo menos 3 de los segmentos dibujados y que no había dibujado ningún triángulo ni ningún cuadrilátero con vértices en los puntos marcados.
Determina el menor número de puntos que pudo haber marcado Patricia y dibuja una posible distribución de los puntos y los segmentos, con este número de puntos.
Explica por qué Patricia no pudo marcar menos puntos.
6
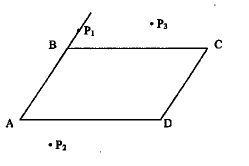
En una hoja blanca Juan dibujó un paralelogramo ABCD y pintó de azul todos los puntos P de la hoja tales que:
área (BPD) = área (APB) + área (BPC)
a) Para cada uno de los puntos P1, P2 y P3, determina si Juan lo pintó de azul y explica por qué.
b) Encuentra toda la región de la hoja que Juan pintó de azul y coloréala. Justifica tu respuesta.
NOTA: si los 3 vértices de un "triángulo" están en una misma recta, su área es igual a 0 (cero).

| nivel 1 |
1
En el triángulo ABC, sean D el punto donde la bisectriz del ángulo ABC intersecta al lado AC y E el punto donde la bisectriz del ángulo BCA intersecta al lado AB. Sean P y Q los puntos donde la recta DE intersecta a la circunferencia circunscrita al triángulo ABC.
Si AP = AQ, demuestra que el triángulo ABC es isósceles.
2
En un tablero cuadriculado de 100 x 100 cada casilla está pintada de blanco o de negro. Las casillas de las esquinas son negras y todas las demás casillas de los bordes (orillas) son blancas.
Diremos que dos casillas son vecinas si tienen por lo menos un vértice común. En cada casilla escribimos el número que es igual a la cantidad de casillas negras vecinas que tiene esa casilla. ¿Es posible que la suma de todos los números escritos en el tablero sea igual a 2000?
3
Cierto país tiene solamente monedas de 1, 2, 3 y 4 centavos, y la entrada al zoológico cuesta 1 centavo. Un grupo de personas se dice afortunado si ningún integrante del grupo tiene monedas de 1 centavo, pero todos tienen monedas de mayor valor, y cuando juntan todas sus monedas pueden pagar sus entradas y cada miembro del grupo recibe el cambio exacto, utilizando solamente monedas de los otros miembros del grupo (sin pedirle al cajero, ni pedir prestado). Un ejemplo de un grupo afortunado es uno de dos personas, una con dos monedas de 2 centavos y la otra con una moneda de 3 centavos. Juntan las tres monedas, pagan las entradas con una moneda de 2 centavos y con las dos monedas restantes reciben su vuelto de 3 centavos y 2 centavos, respectivamente.
Determina el mínimo número de monedas que puede tener, en conjunto, un grupo afortunado de n personas y muestra cómo se pueden distribuir estas monedas entre las n personas.
4
¿Existe un número natural n tal que la suma de los dígitos de n sea divisible por 23 y la suma de los dígitos de (n+1) también sea divisible por 23? Si la respuesta es sí, halla el menor número n. Si es no, explica por qué.
5
Sea ABC un triángulo con AB = AC. Con centro en un punto del lado BC se construye la circunferencia S que es tangente a los lados AB y AC. Sean P y Q puntos cualesquiera sobre los lados AB y AC respectivamente, tales que PQ es tangente a S.
Demuestra que PB . CQ = (BC / 2)2
6
En un tablero cuadriculado, de 2000 filas por 2000 columnas, dos personas, A y B, cada una en su turno, colocan un 1 ó un -1 en una casilla libre. Una vez completado el tablero, se calculan los productos de los números de las 2000 filas, los productos de los números de las 2000 columnas, y se suman los 4000 números así obtenidos. Esta suma final S es el resultado del juego. El objetivo de A es que S sea lo mayor posible y el objetivo de B es que S sea lo menor posible.
En un juego en el que A comienza, determina cuál es el máximo valor de S que puede garantizar A, independientemente de cómo juegue B y cuál es el mínimo valor de S que puede garantizar B, independientemente de cómo juegue A.
| nivel 2 |
1
Sea n > 1 un entero. Calcular la cantidad de permutaciones (p1, p2, ..., pn) de (1, 2, ..., n) tales que pi+1 - pi < 1 para todo i, 1 < i < n - 1.
2
Dado un triángulo ABC, sean D y E puntos interiores de los lados AB y AC respectivamente, tales que B, D, E y C son concíclicos. Sea F la intersección de las rectas BE y CD. Las circunferencias circunscriptas a los triángulos ADF y BCD se cortan en G y en D.
Demostrar que la recta GE corta al segmento AF en su punto medio.
3
Sea m > 3 un entero. Calcular el mínimo entero positivo r con la propiedad: en cada partición del conjunto {1, 2, ..., r} en dos subconjuntos, hay alguno de los subconjuntos en el cual se pueden elegir elementos a1, a2, ..., am (eventualmente repetidos) tales que a1 + a2 + ... + am - 1 = am.
4
Encontrar todas las ternas (x, y, z) de enteros positivos tales que,
1 + 2x + 3y = z3.
5
Se considera un triángulo ABC con los ángulos A y B agudos. Las bisectrices de los ángulos A y B cortan a BC y AC en M y N respectivamente. Sean P y Q puntos del lado AB tales que MP es perpendicular a AB y NQ es perpendicular a AB.
Sabiendo que el ángulo C > 2 . PCQ, calcular la medida del ángulo C.
6
Sea l un segmento con la siguiente propiedad: para cualquier conjunto formado por segmentos rojos y azules tales que la suma de las longitudes de los segmentos rojos es 1 y la suma de las longitudes de los segmentos azules es también 1, hay una forma de ubicar todos los segmentos sobre A de manera que:
Calcular la menor longitud posible de¡ segmento l.
| nivel 3 |
1
Sean a, b y c enteros positivos tales que a2 + b2 + 1 = c2.
Demostrar que [ a / 2 ] + [ c / 2 ] es par.
Nota : [ x ] es la parte entera de x.
2
En un triángulo ABC se consideran los puntos D, E y F sobre los lados BC, CA y AB respectivamente, tales que las áreas de los triángulos AFE, BFD y CDE son iguales.
Demostrar que (DEF) / (ABC) > 1/4
Nota: (XYZ) es el área del triángulo XYZ.
3
Sea n > 2 un entero. Para cada n-upla (x1, x2, ..., xn) tal que x12 + x22 + ... + xn2 = 1 llamamos
m = min { | xi - xj | : 1 < i < j < n}.
Calcular el mayor valor posible de m.
4
Sean a y b enteros positivos tales que el número b2 + (b + l)2 + ... + (b + a)2 - 3 es múltiple de 5 y a + b es impar.
Calcular el dígito de las unidades del número a + b escrito en notación decirnal.
5
Sea ABC un triángulo con AB < AC. Sean L el punto rnedio del arco BC (que no contiene a A) de la circunferencia G circunscripta a ABC y E el punto del lado AC tal que AE = (AB + AC) / 2. La recta LE y la circunferencia G se cortan en L y en P.
Si M y N son los puntos medios de los lados AB y BC respectivamente, demostrar que las rectas AL, BP y MN son concurrentes.
6
Sea j(x) = ax2 + bx + c una función cuadrática con coeficientes reales (a distinto de 0) tal que la ecuación j(j(x)) = x tiene cuatro raíces reales distintas.
Demostrar que no existe ninguna función f : R --> R tal que f (f (x)) = j(x) para todo x real.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |