Clase 3 - Curiosidades pitagóricas

Esperamos sus mails en educabri@oma.org.ar.

 

¿Quién no vio alguna vez el teorema de Pitágoras? Probablemente pocos; pero lo que seguramente no muchos habrán visto es una demostración del mismo. En esta clase veremos esto y otras curiosidades que se derivan de este famoso teorema.

Armemos un rompecabezas para demostrar el teorema de Pitágoras.

1. Construyan un triángulo AIB tal que AIB = 90°.
2. Construyan, ahora, los cuadrados ABCD, AISR y BIKJ exteriores al triángulo AIB.

3. Lo que vamos a hacer ahora es partir el cuadrado BIKJ en 4 piezas para reacomodarlas junto con el cuadrado AISR y formar el cuadrado ABCD.

4. Tracen el centro, O, del cuadrado BIKJ.

5. Construyan por O una paralela a AB, que corta a IK en M y a BJ en U.

6. Tracen por O una perpendicular a AB, que corta a KJ en N y a IB en V; tracen una paralela a AB, que corta a IK en M.

7. Quedan formados cuatro cuadriláteros: VOMI, MONK, NOUJ y UOVB.

8. Traten, ahora, de armar el rompecabezas. ¿Pueden demostrar por qué funciona la construcción?

Veamos ahora una demostración un poco más formal del teorema. Dado un cuadrado ABCD de lado a+b, sean P, Q, R y S puntos sobre los lados como muestra la figura, de modo que AS = BP = CQ = DR = a.

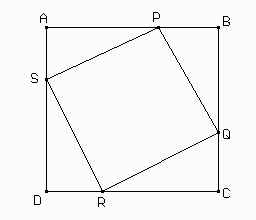
Si quieren hacer la construcción con el Cabri, pueden construir primero el cuadrado ABCD y el punto P sobre AB. Tracen el simétrico de P con respecto a la intersección de las diagonales del cuadrado, llamémosla O, obteniendo así el punto R. La mediatriz de PR determinará con AD y BC los puntos S y Q respectivamente. Intenten probar, ahora, que PQRS es un cuadrado. Fíjense que el problema es parecido al que tratamos en la clase 1. En caso de que no puedan hacerlo, no duden en escribirnos.

Sigamos con nuestra demostración. Supongamos que el lado del cuadrado PQRS es c. El área del cuadrado ABCD es (a+b)² = a² + 2ab + b². El área de cada uno de los triángulos rectángulos es ab/2. Es decir que el área de los cuatro triángulos es igual a 2ab.

Como el área del cuadrado ABCD es igual a la suma de las áreas de los cuatro triángulos rectángulos más el área de PQRS, que es c², entonces planteando la relación obtenemos la siguiente igualdad:

a² + 2ab + b² = 2ab + c²

a² + b² = c² es decir que la suma de los cuadrados de los catetos es igual al cuadrado de la la hipotenusa.

Analicemos, ahora, el siguiente problema y veamos como el teorema de Pitágoras nos facilita las cosas.

Problema 1. Dados dos triángulos equiláteros ABC y DEF, construir un triángulo equilátero PQR cuya área sea igual a la suma de las áreas de ABC y de DEF.

Supongamos que los lados de ABC, DEF y PQR sean x, y y z respectivamente. Calculemos el área de ABC. Sea M el punto medio de AB.

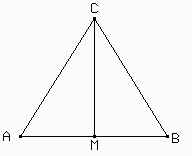
CM es perpendicular a AB, pues C está en la mediatriz de AB. Además AM = MB = x/2. Entonces por el teorema de Pitágoras en el triángulo MCA tenemos que CM² = 3/4 x². Verifíquenlo.

Dado que el área de ABC es igual a CM.AB/2 entonces Área(ABC) = x²./4.

Del mismo modo obtenemos las áreas de DEF y de PQR. Como el área de PQR es igual a la suma de las áreas de DEF y de ABC entonces x²./4 + y²./4 = z²./4. Simplificando tenemos que x² + y² = z². Es decir, los lados de los triángulos cumplen la relación pitagórica. Por tanto, bastará con construir un triángulo equilátero sobre la hipotenusa de un triángulo rectángulo de catetos x e y. Intenten construir la figura.

Problema 2. Dado un rectángulo ABCD y un punto P en su interior. Demostrar la siguiente igualdad: PA² + PC² = PB² + PD².

El hecho de que aparezca en el enunciado una suma de cuadrados nos hace sospechar que en algún momento va a haber que utilizar el teorema de Pitágoras. Pero, ¿cómo?

Tracemos por el punto P dos rectas paralelas a los lados del rectángulo como indica la figura.

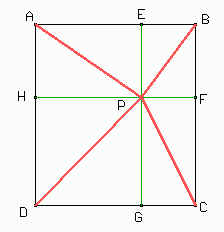
Tenemos que AE = HP = DG = a; EB = PF = GC = b; AH = EP = BF = c y DH = PG = FC = d.

Ahora sí es más fácil ver como se puede utilizar el teorema de Pitágoras. Entonces podemos ver que PA² = a² + c²; PB² = b² + c²; PC² = b² + d² y PD² = a² + d². Sumando llegamos a la igualdad del enunciado PA² + PC² = PB² + PD².

El último problema que vamos a tratar esta clase, es el clásico de calcular longitudes de segmentos. Sin embargo, a diferencia de los problemas que comúnmente nos encontramos, éste se sitúa en el espacio.

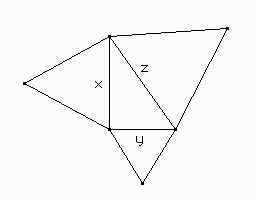
Problema 3. Dado un tetraedro regular ABCD de lado 2 (sus caras son triángulos equiláteros), sean R y S los puntos medios de AB y CD respectivamente. Hallar la longitud de RS.

Antes de comenzar vamos a realizar una figura para aquellos que no están tan familiarizados con los tetraedros.

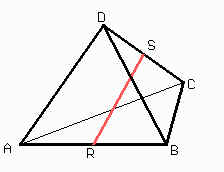
Debido a que SA es una mediana en el triángulo equilátero ADC y SB es una mediana en el triángulo equilátero BCD y ambos triángulos son del mismo tamaño, podemos afirmar entonces que SA = SB.

Es decir, SAB es un triángulo isósceles y como R es el punto medio de la base AB entonces RS es perpendicular a dicha base.

Por tanto, SRB es un triángulo rectángulo con RB = 1 y SB = .¿Por qué? Utilizando, ahora el teorema de Pitágoras en dicho triángulo obtenemos RS = .

Para terminar esta clase les dejamos algunos problemas para que practiquen. Los primeros son más bien sencillos, mientras que los últimos requieren mayor paciencia y dedicación. Cualquier duda que tengan, ¡No duden en escribirnos!

Problemas

1. Construir un cuadrado ABCD y otro EFGH de modo que el segundo tenga 5 veces el área del primero.

2. En una circunferencia, dos cuerdas perpendiculares AB y CD se cortan en un punto E de modo que AE = 3, EB = 2, CE = 1 y ED = 6. Hallar el radio de la circunferencia.

3. Se tiene un ladrillo cuyos lados midan 3, 4 y 12. ¿cuánto mide la diagonal mayor?

4. Demostrar que la suma de los catetos de un triángulo rectángulo es menor o igual que la diagonal del cuadrado construido sobre la hipotenusa.

5. Sea ABCD un paralelogramo y P un punto en su interior tal que PA² + PC² = PB² + PD². Demostrar que ABCD es un rectángulo.

Esta fue la tercer clase de EduCabri 2000, el curso de Cabri por Internet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar