

Clase 9 - Valor intermedio II
Luego del receso invernal continuamos con los temas que dejamos pendientes la clase pasada. Por si no lo recuerdan, habíamos propuesto 4 problemas de los cuales ya resolvimos dos. Esta clase veremos la solución de los dos restantes y algunas ideas relacionadas con dichos problemas. Acá van los enunciados, en caso que se los hayan olvidado:
B. Dado un polígono convexo y un punto P en su interior. Demostrar que existen dos puntos A y B en el borde del polígono de modo que P sea el punto medio de AB.
C. En una ruta un auto recorre 100 km, desde A hacia B, en una hora pero no fue a velocidad constante. Demostrar que hubo algún instante en camino en el que el auto fue a exactamente 100 km/h.
La clase pasada enunciamos un teorema relacionado con funciones que tomaban valores enteros. Ahora veremos otro teorema, más fuerte que el anterior, el teorema de Bolsano:
Sea f una función continua de reales en reales tal que f(a) < 0 y f(b) > 0. Entonces existe un número real c, entre a y b tal que f(c) = 0.
Antes de analizar lo que nos dice el teorema, detengámonos un segundo en un par de cuestiones técnicas. ¿Qué es una función continua? La verdad es que no es nada fácil definirla formalmente pues se requieren algunas nociones de límites y de los axiomas de los números reales, que no es nuestra intención que ustedes sepan a esta altura. Así que nos conformaremos con una definición intuitiva de continuidad:
Diremos que una función es continua si su gráfica se puede recorrer con un lápiz de un sólo trazo. Y, una definición un poco más formal, f(x) se acerca a f(y) cuando x se acerca a y.
Por ejemplo, las siguientes funciones son continuas:
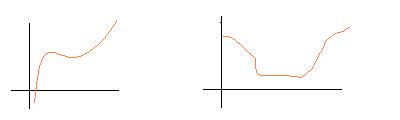
Y las siguientes funciones son discontinuas, es decir no son continuas:
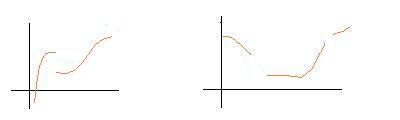
A simple vista resulta bastante obvio que si en algún lugar, la función es negativa, y en otro es positiva, como en el caso de la primer función continua que les mostramos, entonces para algún c f(c) = 0 o lo que es lo mismo, la gráfica corta al eje de las x.
Resulta que la demostración de este teorema no es para nada obvia y de hecho no se cumple siempre, si la función no está definida en reales. Por ejemplo f(x) = x² - 2 definida para x racional cumple que f(1) < 0 y que f(2) > 0, además es continua en los racionales (¡Créannos!) pero no hay ningún racional q tal que f(q) = 0 pues q² - 2 = 0 no tiene solución en los racionales por que raíz de 2 es irracional.
Ejemplos de funciones continuas son:
todos los polinomios
las funciones seno y coseno
las exponenciales
raíz cuadrada de x es continua para todo x > 0
Además las funciones continuas tienen muchas propiedades. Por ejemplo si f(x) y g(x) son funciones continuas, entonces:
f (x) + g(x) es una función continua
f(x) . g(x) es una función continua
f(x) / g(x) es una función continua siempre y cuando g(x) nunca valga cero
Si no vieron este tema antes les sugerimos que se detengan a reflexionar en los siguientes ejercicios:
a) Sea f(x) = x7 + 3x4 - 2x - 3. Demostrar que el polinomio f(x) tiene una raíz positiva.
b) Sea g una función continua tal que g(0) = 1 y g(3) = 2. ¿Puede existir algún c con 0 < c < 3 de modo que g(c) = 0?
c) Sea p(x) = x3 - x2 + x - 1 por lo que p(0) = - 1 y p(2) = 5. Verificar que existe un c entre 0 y 2 tal que p(c) = 0. ¿Cuánto vale c?
d)
Demostrar que la función h(x) = es continua donde f(x) es una función continua y a
y b son números fijos.
Ahora podemos volver a los problemas que propusimos al principio de la clase.
C. Por simplicidad comencemos por el problema C.
Este problema parece muy sencillo a simple vista, pero deja de ser tan fácil cuando tratamos de demostrarlo rigurosamente. Sea h(t) = v(t) - 100 donde v(t) es la velocidad del auto en el instante t. Consideramos como instante 0 el momento en que el coche pasó por A.
Como el auto no fue a velocidad constante en algún momento su velocidad fue superior a 100 km/h y en otro momento su velocidad fue menor a 100 km/h porque si en todo momento la velocidad hubiese sido superior a 100 km/h el coche habría recorrido más de 100 km; y si en todo momento la velocidad hubiese sido menor a 100 km/h el coche habría recorrido menos de 100 km.
Es decir existe a y b tal que v(a) < 100 y v(b) > 100, o lo que es lo mismo h(a) < 0 y h(b) > 0. Además la función velocidad es continua. Para los que saben de física, esto se debe a que se necesitaría infinita fuerza para que en un instante la velocidad salte de un valor a otro.
Entonces estamos en las condiciones del teorema de Bolsano, por lo que existe un c entre a y b tal que h(c) = 0 o lo que es lo mismo v(c) = 100. Es decir, que en el instante c el auto iba a exactamente 100 km/h!!!
B. Este problema es un poco más difícil que el anterior, pero de todas formas sale usando la misma idea que antes. Sea M un punto fijo sobre el polígono. Para cada q entre 0° y 360° hay un punto L sobre el polígono tal que:
Es bastante parecido al método que utilizamos la clase pasada para demostrar que en un conjunto de 2n+2 puntos (en el que no hay 3 alineados) existe una recta que pasa por dos de ellos y deja n puntos de cada lado.
Sea L(q) la distancia desde P al punto L, que depende de q.
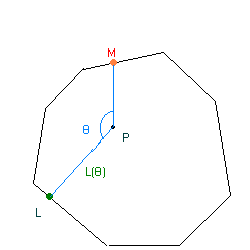
La recta que pasa por L y P interseca, nuevamente, al polígono en K. Sea K(q) la distancia desde P al punto K que se obtuvo en función de q.
Finalmente sea T(q) = L(q) - K(q). Veamos que L(q) y K(q) son continuas usando nuestra definición. Si x es muy pequeño, los dos puntos sobre el polígono están muy próximos y L(q) y L(q + x) están muy cerca también. Entonces L(q) es una función continua; de forma análoga probamos que K(q) es continua. Por lo tanto, T(q) es continua.
Lo que debemos demostrar, entonces, es que existe un q tal que T(q) = 0, ¿por qué?
Sea N la otra intersección de MP y el polígono. Si MP = NP el problema está resuelto. En caso contrario, podemos suponer, sin perdida de generalidad, que MP < NP. Entonces T(0°) = MP - NP < 0, y T(180°) = NP - MP > 0. Entonces por el teorema de Bolsano existe un q entre 0° y 180° tal que T(q) = 0 con lo que queda resuelto el problema.
Fíjense que en ningún momento utilizamos que la figura deba ser un polígono. La única condición que necesitamos es que la figura sea un trazo continuo.
Para terminar les dejamos algunos problemas. ¡¡¡No se olviden de contestar la encuesta que está al final de la clase!!!
Problemas
1. Un vehículo viaja desde A hasta B, que están separadas por 400 km tardando 4 horas. No se sabe a qué velocidad iba en cada instante. Demostrar que hubo un período de 1 hora en el que recorrió 100 km exactamente.
2. Demostrar que un polinomio de grado impar tiene siempre una raíz real.
Comentario: Fíjense que este mismo problema estuvo en la clase de polinomios pero lo resolvimos teniendo en cuenta que las raíces complejas se pueden agrupar de a dos.
3. Sea P un polígono convexo y sea A un punto en su interior.
a) Demostrar que existe una recta que pasa por A que divide al polígono P en dos polígonos de igual perímetro.
b) ¿Puede ser que existan cinco rectas con las mismas propiedades que en a) ?
c) Demostrar que para todo polígono convexo P existe un punto A en su interior tal que hay al menos dos rectas distintas tal que cada una divida al polígono en dos de igual perímetro.
Esta fue la novena clase de Miscelánea, el curso de matemáticas por Internet. Esperamos que les haya gustado. En quince días, ofreceremos una nueva clase.
Ahora, es el turno de ustedes. Queremos que hagan los problemas y ejercicios que fuimos dando a lo largo de la clase. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es misc@oma.org.ar .
También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.
| Internet vía OmaNet www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |