Nota 1 - 10 / 11 / 1998

Esperamos sus mails en problematica@oma.org.ar

Ya está terminando la olimpíada nacional de este año. ¡Les deseamos mucha suerte a todos los que van a participar!

Y ya podemos empezar a entrenar para el año que viene. Así que vamos a abrir este taller con algunos comentarios de los problemas de la intercolegial de este año. (Pueden encontrarlos en http://www.oma.org.ar/enunciados/oma15int.htm )

No vamos a contarles las soluciones, la idea es que ustedes nos las cuenten a nosotros. Pero vamos a dar algunas pistas o algunas cosas que es bueno saber para hacerlos.

Elegimos un problema de cada nivel.

Lo primero que tenemos que saber son las reglas de divisibilidad por estos números. Es decir, cómo sabemos si un número es divisible por 3 o por 5 o por 11...

Empezamos con divisivilidad por 5, que es la más fácil:

Un número es divisible por 5 si termina en 0 o en 5.

Por ejemplo, 23525 es divisible por 5 y 505050501 no es divisible por 5.

Ahora por 3:

Un número es divisible por 3 si la suma de sus cifras es divisible por 3.

Así escrito parece un círculo sin salida, porque ¿cómo sabemos si la suma de sus cifras es divisible por 3? Hacemos lo mismo: sumamos las cifras del resultado de esa suma. Y seguimos sumando hasta obtener un número de una cifra, que para que sea divisible por 3 tiene que ser 0, 3, 6 o 9.

A ver algunos ejemplos:

• 123456789
  La suma es 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45.
  Y la suma de las cifras de 45 es 4 + 5 = 9.
  Entonces es divisible por 3.
  
• 1000000000
  La suma de las cifras es 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 1
  Entonces NO es divisible por 3.
  Esta no era la única forma de verlo. También podíamos notar que 1000000000 = 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 = 10⁹ = 5⁹ x 2⁹, que no es divisible por 3.
  

Antes de ver divisivilidad por 4, hagamos divisibilidad por 2

Un número es divisible por 2 si la última cifra es par (es decir: 0, 2, 4, 6 u 8).

Por ejemplo, 526 es divisble por 2 y 2463 no es divisible por 2.

Ahora sí, la de divisibilidad por 4.

Un número es divisible por 4 si el número formado por las dos últimas cifras es divisible por 4.

Algunos ejemplos:

• 123456789
  El número formado por las dos últimas cifras es 89, que no es divisible por 4. (Podés hacer la cuenta en la calculadora, pero ¡ni siquiera es divisible por 2!)
  
• 1000000000
  El número formado por las dos últimas cifras es 00, o 0, que es divisible por 4. Entonces 1000000000 es divisible por 4.

Y divisibilidad por 11, que es la más difícil, y que muchos no conocen:

Un número es divisible por 11 si la suma de las cifras que ocupan posiciones pares menos la suma de las cifras que ocupan posiciones impares es divisible por 11.

Tal vez tengas que releer varias veces la frase hasta entender lo que dice. Esperamos que con los ejemplos quede más claro:

• 187387582
  Pintemos de verde las cifras en posiciones pares: 187387582. Entonces, la suma de las cifras en posiciones pares es 8 + 3 + 7 + 8 = 26. Y las cifras en posiciones impares son todas las otras. Su suma es 1 + 7 + 8 + 5 + 2 = 23.
  Ahora restamos 26 - 23 = 3, que no es divisible por 11. Entonces 187387582 no es divisible por 11.
  
• 1234554321
  La cuenta que tenemos que hacer es (2 + 4 + 5 + 3 + 1) - (1 + 3 + 5 + 4 + 2) = 0. Entonces 1234554321 es divisible por 11.
  
• ¿Qué pasa con el número def que nos dice el problema? Simplemente, tenemos que ver que e - (d + f) sea divisible por 11. Puede dar negativo, no importa. Por ejemplo, -22 es divisible por 11 y -5 no.

Ahora te toca a vos juntar todo esto y ver cómo podés hacer el problema.

Lo primero que tendríamos que hacer es un dibujo de la figura.

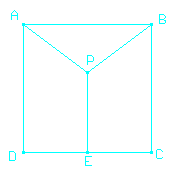
Por los datos que nos dan, el triángulo APB es isósceles. Entonces P tiene que estar en la mediatriz de AB. Y como PE es perpendicular a CD, PE va a ser perpendicular a AB. Entonces, E también está en la mediatriz de AB. Nos queda que E es el punto medio de DC.

Así que el dibujo es más o menos como está arriba. Ahora no se ve muy difícil. Un poco de Pitágoras y debería salir. ¿Te animás a seguir?

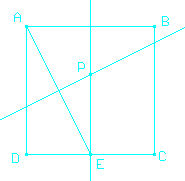
Una pregunta interesante (pero que no importa para resolver el problema) es cómo construir el punto P con regla y compás (o con el Cabri). La clave para eso es notar que el triángulo APE también es isósceles. Entonces P está en la mediatriz de AE.

Los problemas de Pablo Parece que Pablo Picapiedra tiene mucha memoria. Se acuerda de los problemas de hace muchos años. Así que cada vez que algo de lo que charlemos le recuerde a algún problema viejo, nos lo va a contar. Y esto último de lo que hablamos le trajo a la memoria estos problemas, de la regional de la IX Olimpíada Nacional de Matemática. 1. Construir un triángulo isósceles con los siguientes datos: Perímetro = 18 cm Altura correspondiente a la base = 5 cm Indicar los pasos de la construcción. 2. Dibujar un triángulo ABC con los siguientes datos: ÐA = 30º AB = 5 cm AC + CB = 11 cm Indicar los pasos de la construcción.

Así como está el problema, uno no sabe para donde agarrar porque está la n arriba y abajo.

Si estuviera sólo arriba, por ejemplo, (n + 98) / 19, n + 98 tendría que ser múltiplo de 19 y, aunque son infinitos, podemos expresarlos de alguna forma.

Si estuviera sólo abajo, por ejemplo, 98 / (n + 19), n + 19 tendría que ser un divisor de 98 y para cada divisor de 98 encontramos un n.

Queremos llevarlo a alguna de esas dos formas. ¿Se te ocurre cómo?

Un problema parecido a este, pero más difícil, apareció en la primera Olimpíada Internacional de Matemática: Probar que la fracción (21 n + 4) / (14 n + 3) es irreducible para cualquier número natural n.

Acá terminamos por ahora, y esperamos sus mails para seguir avanzando. Teníamos ganas de contar un poco más, pero no queremos "quemarles" los problemas. ¡Será hasta la próxima!

Actividades OmaNet Problemática	OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar